
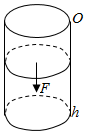
 如图,在某一温度下,直径为0.2m,高为0.8m上端为活塞的圆柱体内某气体的压强p(N/m2)与体积V(m3)的函数关系式为p=$\frac{80}{V}$,而正压力F(N)与压强p(N/m2)的函数关系为F=pS,其中S(m2)为受力面积.设温度保持不变,要使气体的体积缩小为原来的一半.求活塞克服气体压力做多少功?
如图,在某一温度下,直径为0.2m,高为0.8m上端为活塞的圆柱体内某气体的压强p(N/m2)与体积V(m3)的函数关系式为p=$\frac{80}{V}$,而正压力F(N)与压强p(N/m2)的函数关系为F=pS,其中S(m2)为受力面积.设温度保持不变,要使气体的体积缩小为原来的一半.求活塞克服气体压力做多少功?  100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:选择题
| A. | n(n+2) | B. | $\frac{n}{2}$(2n+3) | C. | n(2n+3) | D. | $\frac{n}{2}$(2n+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | -1 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知三棱锥的三视图如图所示,其中侧视图是边长为$\sqrt{3}$的正三角形,则该几何体的外接球的体积为( )
已知三棱锥的三视图如图所示,其中侧视图是边长为$\sqrt{3}$的正三角形,则该几何体的外接球的体积为( )| A. | $\frac{16π}{3}$ | B. | $\frac{32}{3}π$ | C. | 4$\sqrt{3}$π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
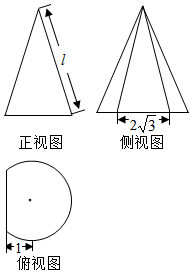 如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | $\sqrt{2}+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com