
分析 设圆的半径为1,则S圆=π,S正三角形ABC=$\frac{3\sqrt{3}}{4}$,根据概率公式计算即可.
解答 解:设圆的半径为1,则S圆=π,
S正三角形ABC=3×$\frac{1}{2}$×1×1×sin120°=$\frac{3\sqrt{3}}{4}$.
∴随机向圆所在区域投一点,
则该点恰好落在△ABC内的概率P=$\frac{{3\sqrt{3}}}{4π}$,
故答案为:$\frac{{3\sqrt{3}}}{4π}$.
点评 本题给出几何概型,求点恰好落在△ABC内的概率.着重考查了正三角形的性质、三角形与圆的面积计算和几何概型的计算等知识,属于基础题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
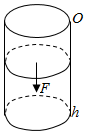 如图,在某一温度下,直径为0.2m,高为0.8m上端为活塞的圆柱体内某气体的压强p(N/m2)与体积V(m3)的函数关系式为p=$\frac{80}{V}$,而正压力F(N)与压强p(N/m2)的函数关系为F=pS,其中S(m2)为受力面积.设温度保持不变,要使气体的体积缩小为原来的一半.求活塞克服气体压力做多少功?
如图,在某一温度下,直径为0.2m,高为0.8m上端为活塞的圆柱体内某气体的压强p(N/m2)与体积V(m3)的函数关系式为p=$\frac{80}{V}$,而正压力F(N)与压强p(N/m2)的函数关系为F=pS,其中S(m2)为受力面积.设温度保持不变,要使气体的体积缩小为原来的一半.求活塞克服气体压力做多少功?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
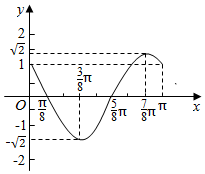
| A. | f(x)=2cos(2x+$\frac{π}{4}$) | B. | f(x)=-$\sqrt{2}$cos(x-$\frac{π}{4}$) | C. | f(x)=-$\sqrt{2}$cos(2x-$\frac{3π}{4}$) | D. | f(x)=$\sqrt{2}$cos(2x-$\frac{π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2}{7}$) | B. | ($\frac{2}{7}$,$\frac{2}{3}$) | C. | ($\frac{2}{3}$,$\frac{4}{5}$) | D. | ($\frac{2}{7}$,$\frac{4}{5}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
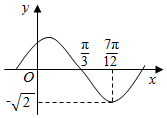 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则$f(\frac{11π}{24})$的值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则$f(\frac{11π}{24})$的值为( )| A. | $-\frac{{\sqrt{6}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com