Question

5．已知边长为2的正方形SG₁G₂G₃，E，F分别是G₁G₂，G₂G₃的中点，SG₂交EF于点D，现沿着线段SE，SF，EF翻折成四面体，使G₁，G₂，G₃重合于点G，则四面体S-EFG中有：（A）SD⊥平面EFG；（B）SG⊥平面EFG；（C）GF⊥平面SGF；（D）GD⊥平面SEF．
（1）画出四面体的草图，并在（A）（B）（C）（D）四个结论中选择你认为正确的结论，加以证明；
（2）求四面体S-EFG的体积．

Answer 1

分析 （1）由题意画出原正方形，结合原正方形画出折叠后的四面体的草图，并得到SG⊥平面EFG，然后由线面垂直的判定加以证明；
（2）由题意可得，三棱锥S-EFG的底面为等腰直角三角形，且由（1）可知SG为三棱锥的高，再由棱锥体积公式求得四面体S-EFG的体积．

解答 解：（1）草图如图，
选B，
事实上，∵SG⊥GF，SG⊥GE，且GF∩GE=G，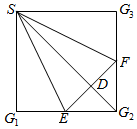
∴SG⊥平面EFG；
（2）∵正方形SG₁G₂G₃的边长为2，且E，F分别是G₁G₂，G₂G₃的中点，
∴EG₂=FG₂=1，
底面△GEF为等腰直角三角形，且由（1）知，SG为三棱锥S-EFG的高，SG=1，
∴${V_{S-}}_{EFG}=\frac{1}{3}{S_{△EFG}}•SG$=$\frac{1}{3}$×$\frac{1}{2}$×1×1×2=$\frac{1}{3}$．
∴四面体S-EFG的体积为$\frac{1}{3}$．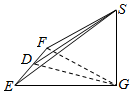

点评 本题考查柱、锥、台体的体积，解答此题的关键是注意折叠问题在折叠前后的变量与不变量，考查空间想象能力与计算能力，是中档题．