
| A. | f(x)=2cos(2x+$\frac{π}{4}$) | B. | f(x)=-$\sqrt{2}$cos(x-$\frac{π}{4}$) | C. | f(x)=-$\sqrt{2}$cos(2x-$\frac{3π}{4}$) | D. | f(x)=$\sqrt{2}$cos(2x-$\frac{π}{4}$) |
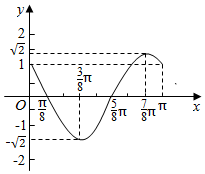
分析 由函数图象知A,T,利用周期公式即可解得ω,又f($\frac{7π}{8}$)=$\sqrt{2}$,解得φ,由诱导公式可得函数的解析式.
解答 解:由函数图象知A=$\sqrt{2}$,$\frac{T}{2}$=$\frac{7π}{8}$-$\frac{3π}{8}$,解得:T=$\frac{2π}{ω}$=π,可得:ω=2,
从而,有f(x)=$\sqrt{2}$cos(2x+φ),
又f($\frac{7π}{8}$)=$\sqrt{2}$cos(2×$\frac{7π}{8}$+φ)=$\sqrt{2}$,
解得:φ=2kπ-$\frac{7π}{4}$,k∈Z,
所以:函数的解析式:f(x)=$\sqrt{2}$cos(2x+2kπ-$\frac{7π}{4}$),k∈Z,
当k=0时,可得f(x)=$\sqrt{2}$cos(2x-$\frac{7π}{4}$)=-$\sqrt{2}$cos(2x-$\frac{3π}{4}$).
故选:C.
点评 本题主要考察了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了诱导公式及数形结合思想的应用,属于基础题.


科目:高中数学 来源: 题型:选择题
 已知三棱锥的三视图如图所示,其中侧视图是边长为$\sqrt{3}$的正三角形,则该几何体的外接球的体积为( )
已知三棱锥的三视图如图所示,其中侧视图是边长为$\sqrt{3}$的正三角形,则该几何体的外接球的体积为( )| A. | $\frac{16π}{3}$ | B. | $\frac{32}{3}π$ | C. | 4$\sqrt{3}$π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
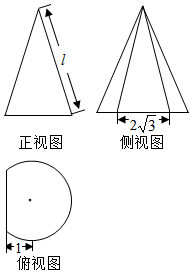 如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )
如图所示是沿圆锥的两条母线将圆锥削去一部分后所得几何体的三视图,其体积为$\frac{16π}{9}+\frac{{2\sqrt{3}}}{3}$,则圆锥的母线长为( )| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | 4 | D. | $\sqrt{2}+\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
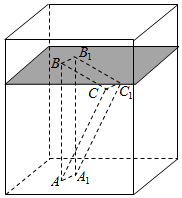 已知三棱柱ABC-A1B1C1,侧棱BB1⊥平面ABC,AB=2,AC=$\sqrt{3}$,AA1=$\frac{1}{4}$,AC⊥BC,将其放入一个水平放置的水槽中,使AA1在水槽底面内,平面ABB1A1与水槽底面垂直,且水面恰好经过棱BB1,现水槽底面出现一个洞,水位下降,则在水位下降过程中,几何体露出水面部分的面积S关于水位下降的高度h的图象大致为( )
已知三棱柱ABC-A1B1C1,侧棱BB1⊥平面ABC,AB=2,AC=$\sqrt{3}$,AA1=$\frac{1}{4}$,AC⊥BC,将其放入一个水平放置的水槽中,使AA1在水槽底面内,平面ABB1A1与水槽底面垂直,且水面恰好经过棱BB1,现水槽底面出现一个洞,水位下降,则在水位下降过程中,几何体露出水面部分的面积S关于水位下降的高度h的图象大致为( )| A. | 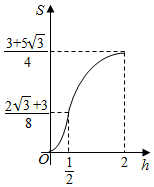 | B. | 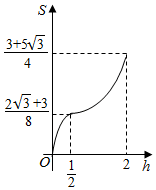 | ||
| C. | 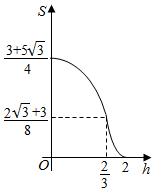 | D. | 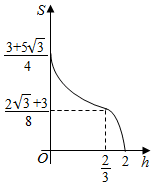 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | $-\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com