
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{5}{4}$ | D. | 2 |
分析 设P(x0,y0),M(x1,y1),则N(x2,y2).利用kPMkPN=$\frac{5}{4}$,化简,结合平方差法求解双曲线C的离心率.
解答 解:由双曲线的对称性知,可设P(x0,y0),M(x1,y1),则N(x2,y2).
由kPMkPN=$\frac{5}{4}$,可得:$\frac{{{y_0}-{y_1}}}{{{x_0}-{x_1}}}•\frac{{{y_0}+{y_1}}}{{{x_0}+{x_1}}}=\frac{5}{4}$,即$y_0^2-y_1^2=\frac{5}{4}(x_0^2-x_1^2)$,即$\frac{5}{4}x_0^2-y_0^2=\frac{5}{4}x_1^2-y_1^2$,
又因为P(x0,y0),M(x1,y1)均在双曲线上,
所以$\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}=1$,$\frac{x_1^2}{a^2}-\frac{y_1^2}{b^2}=1$,所以${a^2}=\frac{4}{5},{b^2}=1$,
所以c2=a2+b2=$\frac{9}{5}$,所以双曲线C的离心率为e=$\frac{c}{a}$=$\frac{\frac{3}{\sqrt{5}}}{\frac{2}{\sqrt{5}}}$=$\frac{3}{2}$.
故选:A.
点评 本题考查双曲线的简单性质的应用,平方差法的应用,考查计算能力.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-x3,x∈R | B. | y=lg|x|,x≠0 | C. | y=x+$\frac{1}{x}$,x≠0 | D. | y=($\frac{1}{2}$)x,x∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
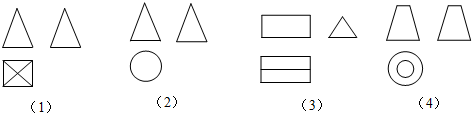
| A. | 四棱台、圆锥、三棱柱、圆台 | B. | 三棱锥、圆锥、三棱台、圆台 | ||
| C. | 四棱锥、圆锥、三棱柱、圆台 | D. | 三棱柱、三棱台、圆锥、圆台 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 100元 | B. | 200元 | C. | 300元 | D. | 400元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com