
| A. | y=-x3,x∈R | B. | y=lg|x|,x≠0 | C. | y=x+$\frac{1}{x}$,x≠0 | D. | y=($\frac{1}{2}$)x,x∈R |
分析 根据奇函数、偶函数及函数单调性的定义,以及根据导数符号判断函数单调性的方法便可判断每个选项的函数的奇偶性和单调性,从而找出正确选项.
解答 解:A.y=-x3为奇函数,且x增大时,y减小;
∴该函数为定义域R上的减函数,∴该选项正确;
B.y=lg|x|为定义域{x|x≠0}上的偶函数,∴该选项错误;
C.$y′=\frac{{x}^{2}-1}{{x}^{2}}$;
∴x∈(-∞,-1),(1,+∞)时,y′>0,x∈(-1,1)时,y′<0;
∴函数y=$x+\frac{1}{x}$在定义域{x|x≠0}上没有单调性,∴该选项错误;
D.$y=(\frac{1}{2})^{x}$的图象不关于原点对称,不是奇函数,∴该选项错误.
故选:A.
点评 考查奇函数、偶函数的定义,减函数的定义,以及根据导数符号判断函数单调性的方法,奇函数图象的对称性,熟悉指数函数的图象.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:选择题
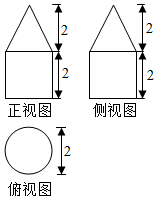
| A. | (5+$\sqrt{5}$)πcm2 | B. | (5+2$\sqrt{5}$)πcm2 | C. | (6+$\sqrt{5}$)πcm2 | D. | (6+2$\sqrt{5}$)πcm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
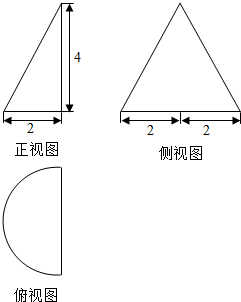
| A. | $\frac{4}{3}π$ | B. | $\frac{8}{3}π$ | C. | $\frac{16}{3}π$ | D. | $\frac{32}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | $\frac{5}{4}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com