
分析 (Ⅰ)利用$4{S_n}={a_n}^2+2{a_n},n∈{N^*}$与4Sn-1=${{a}_{n-1}}^{2}$+2an-1,n≥2作差整理可知an-an-1=2(n≥2),进而可知数列{an}是首项、公差均为2的等差数列,计算即得结论;
(Ⅱ)通过(I)可知数列{bn}是首项、公比均为$\frac{1}{4}$的等比数列,利用等比数列的求和公式可知Tn∈($\frac{1}{4}$,$\frac{1}{3}$),解不等式即得结论.
解答 解:(Ⅰ)∵$4{S_n}={a_n}^2+2{a_n},n∈{N^*}$,
∴4Sn-1=${{a}_{n-1}}^{2}$+2an-1,n≥2,
两式相减得:4an=${{a}_{n}}^{2}$-${{a}_{n-1}}^{2}$+2an-2an-1,
整理得:${{a}_{n}}^{2}$-${{a}_{n-1}}^{2}$=2(an+an-1),
又∵an>0,
∴an-an-1=2(n≥2),
又∵4S1=${{a}_{1}}^{2}$+2a1,解得:a1=2或a1=0(舍),
∴数列{an}是首项、公差均为2的等差数列,
故其通项公式an=2+2(n-1)=2n;
(Ⅱ)由(I)可知${b_n}={({\frac{1}{2}})^{a_n}}$=$\frac{1}{{4}^{n}}$,
∴数列{bn}是首项、公比均为$\frac{1}{4}$的等比数列,
故Tn=$\frac{\frac{1}{4}(1-\frac{1}{{4}^{n}})}{1-\frac{1}{4}}$=$\frac{1}{3}$(1-$\frac{1}{{4}^{n}}$)∈($\frac{1}{4}$,$\frac{1}{3}$),
∴$\frac{1}{m+3}$≤$\frac{1}{4}$,且$\frac{1}{3}$≤m2-6m+$\frac{25}{3}$,
∴m≥1,且m≤2或m≥4,
故1≤m≤2.
点评 本题考查数列的通项及前n项和,考查运算求解能力,涉及解不等式,注意解题方法的积累,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-x3,x∈R | B. | y=lg|x|,x≠0 | C. | y=x+$\frac{1}{x}$,x≠0 | D. | y=($\frac{1}{2}$)x,x∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
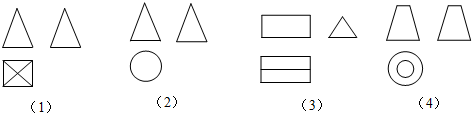
| A. | 四棱台、圆锥、三棱柱、圆台 | B. | 三棱锥、圆锥、三棱台、圆台 | ||
| C. | 四棱锥、圆锥、三棱柱、圆台 | D. | 三棱柱、三棱台、圆锥、圆台 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
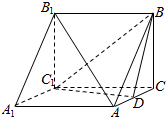 在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,BC⊥AC,BC=AC=2,AA1=3,D为棱AC的中点.
在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,BC⊥AC,BC=AC=2,AA1=3,D为棱AC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com