
分析 (1)直接结合圆的参数方程化为普通方程,然后,结合向量关系,确定令一曲线的普通方程即可;
(2)首先,将所给的直线的极坐标方程化为直角坐标方程,然后,结合直线与圆的位置关系,确定其最大值即可.
解答 解:(1)根据曲线C1的参数方程为$\left\{\begin{array}{l}{x=1+\sqrt{2}cosθ}\\{y=2+\sqrt{2}sinθ}\end{array}\right.$(θ为参数),得
(x-1)2+(y-2)2=2,
设M(x0,y0),点P(x,y),则
(x0-1)2+(y0-2)2=2,
$\overrightarrow{OP}$=(x,y),$\overrightarrow{OM}$=(x0,y0),
∵$\overrightarrow{OP}$=3$\overrightarrow{OM}$.
∴$\left\{\begin{array}{l}{x=3{x}_{0}}\\{y=3{y}_{0}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}_{0}=\frac{x}{3}}\\{{y}_{0}=\frac{y}{3}}\end{array}\right.$,
∴(x-3)2+(y-6)2=18,
∴曲线C2的普通方程:(x-3)2+(y-6)2=18,
(2)根据直线l:ρsinθ-ρcosθ-7=0,得
x-y+7=0,
∵S△MEF=$\frac{1}{2}$|EF|×d(d为M到直线EF的距离),
d的最大值为$\sqrt{2}$+$\frac{|1-2+7|}{\sqrt{2}}$=$\sqrt{2}$+3$\sqrt{2}$=4$\sqrt{2}$,
此时(S△MEF)max=$\frac{1}{2}$|EF|×d=$\frac{1}{2}$×4$\sqrt{2}$×4$\sqrt{2}$=16.
∴△MEF的最大值16.
点评 本题综合考查了直线的极坐标方程、直线与圆的位置关系、圆的参数方程等知识,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
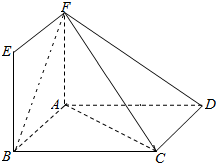 在如图所示的几何体中,四边形ABCD为平行四边形,平面ABEF⊥平面ABCD,∠ACD=90°,AB=2,AD=4,ABEF为正方形,平面ABEF⊥平面ABCD,AN⊥CF,垂足为N.
在如图所示的几何体中,四边形ABCD为平行四边形,平面ABEF⊥平面ABCD,∠ACD=90°,AB=2,AD=4,ABEF为正方形,平面ABEF⊥平面ABCD,AN⊥CF,垂足为N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-x3,x∈R | B. | y=lg|x|,x≠0 | C. | y=x+$\frac{1}{x}$,x≠0 | D. | y=($\frac{1}{2}$)x,x∈R |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com