
在底面半径为6的圆柱内,有两个半径也为6的球面,两球的球心距为13,若作一个平面与两个球都相切,且与圆柱面相交成一椭圆,则椭圆的长轴长为 .
13
【解析】
试题分析:设两个球的球心分别为O1、O2,椭圆的长轴为AB,作出由AB与O1O2确定平面α与两个球及圆柱的截面,并过A作O1O2的垂线,交圆柱的母线于点C,连接O1与AB切球O1的切点D.分别在Rt△O1DE中和Rt△ABC中,利用∠BAC=∠DO1E和余弦的定义,结合题中的数据建立关系式,即可解出AB的长,即得该椭圆的长轴长.
【解析】
设两个球的球心分别为O1、O2,所得椭圆的长轴为AB,
直线AB与O1O2交于点E,设它们确定平面α,
作出平面α与两个球及圆柱的截面,如图所示
过A作O1O2的垂线,交圆柱的母线于点C,设AB切球O1的大圆于点D,连接O1D
∵Rt△O1DE中,O1E= O1O2=
O1O2= ,O1D=6
,O1D=6
∴cos∠DO1E=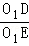 =
=
∵锐角∠DO1E与∠BAC的两边对应互相垂直
∴∠BAC=∠DO1E,
得Rt△ABC中,cos∠BAC= =
=
∵AC长等于球O1的直径,得AC=12
∴椭圆的长轴AB=13
故答案为:13



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.3线性变换的基本性质练习卷(解析版) 题型:选择题
圆x2+y2=1在矩阵A对应的伸压变换下变为椭圆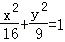 ,则矩阵A是( )
,则矩阵A是( )
A.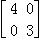 B.
B. C.
C. D.
D.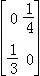
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:填空题
在同一坐标系中,将曲线y=2sin3x变为曲线y=sinx的伸缩变换是
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
正弦曲线y=sinx通过坐标变换公式 ,变换得到的新曲线为( )
,变换得到的新曲线为( )
A.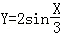 B.Y=2sin3X C.
B.Y=2sin3X C.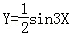 D.
D.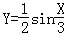
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.3平面与圆锥面的截线练习卷(解析版) 题型:解答题
(2010•顺义区一模)已知椭圆C: ,(a>b>0)的两焦点分别为F1、F2,
,(a>b>0)的两焦点分别为F1、F2, ,离心率
,离心率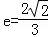 .过直线l:
.过直线l: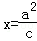 上任意一点M,引椭圆C的两条切线,切点为A、B.
上任意一点M,引椭圆C的两条切线,切点为A、B.
(1)在圆中有如下结论:“过圆x2+y2=r2上一点P(x0,y0)处的切线方程为:x0x+y0y=r2”.由上述结论类比得到:“过椭圆 (a>b>0),上一点P(x0,y0)处的切线方程”(只写类比结论,不必证明).
(a>b>0),上一点P(x0,y0)处的切线方程”(只写类比结论,不必证明).
(2)利用(1)中的结论证明直线AB恒过定点( );
);
(3)当点M的纵坐标为1时,求△ABM的面积.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:填空题
工人师傅在如图1的一块矩形铁皮的中间画了一条曲线,并沿曲线剪开,将所得的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.对工人师傅所画的曲线,有如下说法:
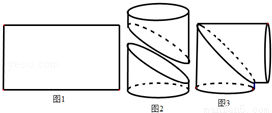
(1)是一段抛物线;
(2)是一段双曲线;
(3)是一段正弦曲线;
(4)是一段余弦曲线;
(5)是一段圆弧.
则正确的说法序号是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.1平行射影练习卷(解析版) 题型:填空题
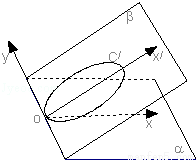
如图,直角坐标系x'oy所在的平面为β,直角坐标系xoy所在的平面为α,且二面角α﹣y轴﹣β的大小等于30°.已知β内的曲线C'的方程是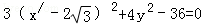 ,则曲线C'在α内的射影的曲线方程是 .
,则曲线C'在α内的射影的曲线方程是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:选择题
已知如图,四边形ABCD为圆内接四边形,AB是直径,MN切⊙O于C点,∠BCM=38°,那么∠ABC的度数是( )

A.38° B.52° C.68° D.42°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷(解析版) 题型:选择题
(文)下列说法中正确的是( )
A.合情推理就是类比推理
B.归纳推理是从一般到特殊的推理
C.合情推理就是归纳推理
D.类比推理是从特殊到特殊的推理
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com