
工人师傅在如图1的一块矩形铁皮的中间画了一条曲线,并沿曲线剪开,将所得的两部分卷成圆柱状,如图2,然后将其对接,可做成一个直角的“拐脖”,如图3.对工人师傅所画的曲线,有如下说法:
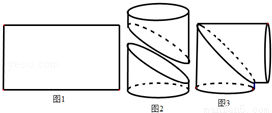
(1)是一段抛物线;
(2)是一段双曲线;
(3)是一段正弦曲线;
(4)是一段余弦曲线;
(5)是一段圆弧.
则正确的说法序号是 .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.3线性变换的基本性质练习卷(解析版) 题型:选择题
已知A(0,0),B(2,0),C(1,2)对△ABC依次作矩阵 对应的变换,变换后的图形面积为( )
对应的变换,变换后的图形面积为( )
A.2 B.6 C.12 D.24
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
变换
 =
=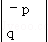 的几何意义为( )
的几何意义为( )
A.关于x轴反射变换 B.关于y轴反射变换
C.关于y=x反射变换 D.关于y=﹣x反射变换
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
(2011•温州二模)将函数y=﹣sinx(x∈[0,π])的图象绕原点顺时针方向旋转角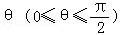 得到曲线C,对于每一个旋转角θ,曲线C都是一个函数的图象,则θ的最大值是( )
得到曲线C,对于每一个旋转角θ,曲线C都是一个函数的图象,则θ的最大值是( )
A. B.
B.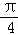 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:填空题
在底面半径为6的圆柱内,有两个半径也为6的球面,两球的球心距为13,若作一个平面与两个球都相切,且与圆柱面相交成一椭圆,则椭圆的长轴长为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷(解析版) 题型:选择题
已知圆柱的底面半径为2,高为3,用一个与底面不平行的平面去截,若所截得的截面为椭圆,则椭圆的离心率的最大值为( )
A.1 B.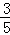 C.
C.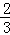 D.
D.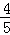
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.1平行射影练习卷(解析版) 题型:选择题
(2005•静安区一模)Rt△ABC的直角边AB在平面α内,顶点C在平面α外,则直角边BC、斜边AC在平面α上的射影与直角边AB组成的图形是( )
A.线段或锐角三角形
B.线段与直角三角形
C.线段或钝角三角形
D.线段、锐角三角形、直角三角形或钝角三角形
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:选择题
PT切⊙O于T,割线PAB经过O点交⊙O于A、B,若PT=4,PA=2,则cos∠BPT=( )
A.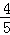 B.
B.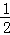 C.
C.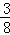 D.
D.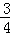
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷(解析版) 题型:选择题
下面对命题“函数f(x)=x+ 是奇函数”的证明不是综合法的是( )
是奇函数”的证明不是综合法的是( )
A.?x∈R且x≠0有f(﹣x)=(﹣x)+ =﹣(x+
=﹣(x+ )=﹣f(x),∴f(x)是奇函数
)=﹣f(x),∴f(x)是奇函数
B.?x∈R且x≠0有f(x)+f(﹣x)=x+ +(﹣x)+(﹣
+(﹣x)+(﹣ )=0,∴f(x)=﹣f(﹣x),∴f(x)是奇函数
)=0,∴f(x)=﹣f(﹣x),∴f(x)是奇函数
C.?x∈R且x≠0,∵f(x)≠0,∴ =
= =﹣1,∴f(﹣x)=﹣f(x),∴f(x)是奇函数
=﹣1,∴f(﹣x)=﹣f(x),∴f(x)是奇函数
D.取x=﹣1,f(﹣1)=﹣1+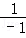 =﹣2,又f(1)=1+
=﹣2,又f(1)=1+ =2
=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com