
��2010•˳����һģ����֪��ԲC�� ����a��b��0����������ֱ�ΪF1��F2��
����a��b��0����������ֱ�ΪF1��F2�� ��������
��������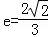 ����ֱ��l��
����ֱ��l��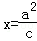 ������һ��M������ԲC���������ߣ��е�ΪA��B��
������һ��M������ԲC���������ߣ��е�ΪA��B��
��1����Բ�������½��ۣ�����Բx2+y2=r2��һ��P��x0��y0���������߷���Ϊ��x0x+y0y=r2����������������ȵõ���������Բ ��a��b��0������һ��P��x0��y0���������߷��̡���ֻд��Ƚ��ۣ�����֤������
��a��b��0������һ��P��x0��y0���������߷��̡���ֻд��Ƚ��ۣ�����֤������
��2�����ã�1���еĽ���֤��ֱ��AB������㣨 ����
����
��3������M��������Ϊ1ʱ�����ABM�������
��1������������2������������3��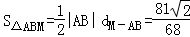
��������
�����������1���ɹ�Բ��һ������߷��̣����Dz�������ƶϳ�����Բ��һ������߷��̣�
��2���ɣ�1���Ľ��ۣ����ǿ������A��B��������꣬�г����߷��̣�����MΪֱ��l��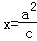 ������һ�㣬�ʿ�֪MΪ����������l�Ĺ������㣬���κô𰸣�
������һ�㣬�ʿ�֪MΪ����������l�Ĺ������㣬���κô𰸣�
��3���ɣ�2���н��ۣ����ǿɵ�M������꣬����l�ķ������ǿ��Լ����AB���ϵĸߣ������ҳ���ʽ�����AB�ij��ȣ����������������ʽ���ɣ�
��������
��1����ȹ�Բ��һ������߷��̣��ɺ���������
����Բ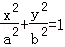 ��a��b��0������һ��P��x0��y0���������߷���Ϊ
��a��b��0������һ��P��x0��y0���������߷���Ϊ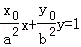 ��
��
��2����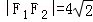 ��������
��������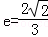
��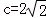 ��a=3��b=1
��a=3��b=1
����ԲC�ķ���Ϊ��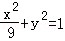
l�ķ���Ϊ��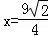
��A��x1��y1����B��x2��y2����M��������Ϊt����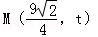 ��
��
�ɣ�1���Ľ���
��MA�ķ���Ϊ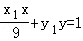
�����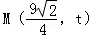 �㣬
�㣬
��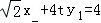
ͬ����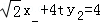
���A��x1��y1����B��x2��y2����ֱ��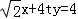 �ϣ�
�ϣ�
��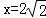 ��y=0ʱ������
��y=0ʱ������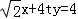 �������
�������
��ֱ��AB������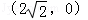
��3��t=1��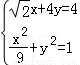 ��ȥy��
��ȥy��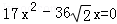 ��
��
��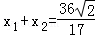 ��x1x2=0��
��x1x2=0��
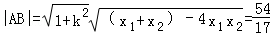
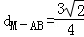
��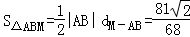 ��
��


 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��[ͬ��]2014�����˽�A��ѡ��4-2 1.3���Ա任�Ļ���������ϰ���������棩 ���ͣ������
��2014•��ģ����֪��M��3����1����ԭ�㰴��ʱ����ת90������ھ���A= ��Ӧ�ı任�����£��õ���N��3��5������a��b��ֵ��
��Ӧ�ı任�����£��õ���N��3��5������a��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014�����˽�A��ѡ��4-2 1.1���Ա任���������ϰ���������棩 ���ͣ������
��ͬһƽ��ֱ������ϵ�У�ֱ��x��2y=2���ֱ��2x�䩁y��=4�������任��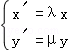 ���+��= ��
���+��= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014�����˽�A��ѡ��4-2 1.1���Ա任���������ϰ���������棩 ���ͣ�ѡ����
��Բx2+y2=4��ÿ����ĺ����겻�䣮����������Ϊԭ���� �����������ߵķ����ǣ� ��
�����������ߵķ����ǣ� ��
A.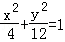 B.
B.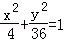 C.
C.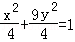 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014�����˽�A��ѡ��4-2 1.1���Ա任���������ϰ���������棩 ���ͣ�ѡ����
��ֱ��y=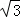 x��ԭ����ʱ����ת60�㣬���õ���ֱ��Ϊ�� ��
x��ԭ����ʱ����ת60�㣬���õ���ֱ��Ϊ�� ��
A.x=0 B.y=0 C.y=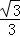 x D.y=��
x D.y=��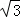 x
x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014�����˽�A��ѡ��4-1 3.2ƽ����Բ����Ľ�����ϰ���������棩 ���ͣ������
�ڵ���뾶Ϊ6��Բ���ڣ��������뾶ҲΪ6�����棬��������ľ�Ϊ13������һ��ƽ�������������У�����Բ�����ཻ��һ��Բ������Բ�ij��᳤Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014�����˽�A��ѡ��4-1 3.2ƽ����Բ����Ľ�����ϰ���������棩 ���ͣ������
��2003•��������ͼ����֪����뾶Ϊr��Բ����һ��ƽ�����أ�ʣ�²���ĸ�߳������ֵΪa����СֵΪb����ôԲ�����غ�ʣ�²��ֵ������ ��
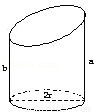
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014�����˽�A��ѡ��4-1 2.4���нǵ�������ϰ���������棩 ���ͣ������
��2014•������ģ����ͼ����֪PA�ǡ�O�����ߣ�AΪ�е㣮PC�ǡ�O��һ�����ߣ�����O��B��C���㣬��Q����BC���е㣮��Բ��O�ڡ�APB�ڲ������OPQ+��PAQ�Ķ���Ϊ ��
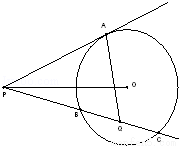
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��[ͬ��]2014�����˽�A��ѡ��4-1 2.1Բ�ܽǶ�����ϰ���������棩 ���ͣ�ѡ����
�ڡ�O�У���AB=1.8cm��Բ�ܽǡ�ACB=30�㣬���O��ֱ�����ڣ� ��
A.3.2cm B.3.4cm C.3.6cm D.4.0cm
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com