
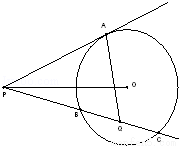
(2014•陕西二模)如图,已知PA是⊙O的切线,A为切点.PC是⊙O的一条割线,交⊙O于B,C两点,点Q是弦BC的中点.若圆心O在∠APB内部,则∠OPQ+∠PAQ的度数为 .
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.3平面与圆锥面的截线练习卷(解析版) 题型:解答题
(2010•顺义区一模)已知椭圆C: ,(a>b>0)的两焦点分别为F1、F2,
,(a>b>0)的两焦点分别为F1、F2, ,离心率
,离心率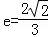 .过直线l:
.过直线l: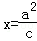 上任意一点M,引椭圆C的两条切线,切点为A、B.
上任意一点M,引椭圆C的两条切线,切点为A、B.
(1)在圆中有如下结论:“过圆x2+y2=r2上一点P(x0,y0)处的切线方程为:x0x+y0y=r2”.由上述结论类比得到:“过椭圆 (a>b>0),上一点P(x0,y0)处的切线方程”(只写类比结论,不必证明).
(a>b>0),上一点P(x0,y0)处的切线方程”(只写类比结论,不必证明).
(2)利用(1)中的结论证明直线AB恒过定点( );
);
(3)当点M的纵坐标为1时,求△ABM的面积.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.1平行射影练习卷(解析版) 题型:填空题
如图,直角坐标系x'oy所在的平面为β,直角坐标系xoy所在的平面为α,且二面角α﹣y轴﹣β的大小等于30°.已知β内的曲线C'的方程是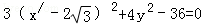 ,则曲线C'在α内的射影的曲线方程是 .
,则曲线C'在α内的射影的曲线方程是 .
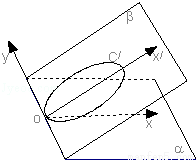
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:填空题
(2014•咸阳二模)如图,已知P是圆O外一点,PA为 圆O的切线.A为切点.割线PBC经过圆心O,若PA=3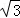 ,PC=9,则∠ACP= .
,PC=9,则∠ACP= .
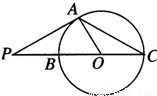
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:选择题
已知如图,四边形ABCD为圆内接四边形,AB是直径,MN切⊙O于C点,∠BCM=38°,那么∠ABC的度数是( )

A.38° B.52° C.68° D.42°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:选择题
如图,AB是半圆O的直径,C、D是半圆上的两点,半圆O的切线PC交AB的延长线于点P,∠PCB=25°,则∠ADC为( )
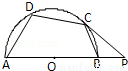
A.105° B.115° C.120° D.125°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷(解析版) 题型:填空题
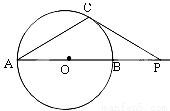
(2012•惠州一模)如图,AB是⊙O的直径,P是AB延长线上的一点.过P作⊙O的切线,切点为C,PC=2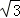 ,若∠CAP=30°,则⊙O的直径AB= .
,若∠CAP=30°,则⊙O的直径AB= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 3.2数学证明练习卷(解析版) 题型:选择题
(2014•泉州模拟)若函数y=f(x)满足:集合A={f(n)|n∈N*}中至少有三个不同的数成等差数列,则称函数f(x)是“等差源函数”,则下列四个函数中,“等差源函数”的个数是( )
①y=2x+1;
②y=log2x;
③y=2x+1;
④y=sin( x+
x+ )
)
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com