练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

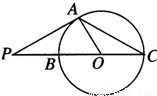
    （2014•咸阳二模）如图，已知P是圆O外一点，PA为 圆O的切线．A为切点．割线PBC经过圆心O，若PA=3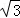，PC=9，则∠ACP= ．

     

     

    30°

    【解析】

    试题分析：利用切割线定理计算出PB，从而可得OA=3，OP=6，∠AOP=60°，即可求出∠ACP．

    【解析】
    ∵PA为圆O的切线，A为切点，割线PBC经过圆心O，

    ∴PA2=PB•PC，

    ∵PA=3，PC=9，

    ∴27=9PB，∴PB=3，∴BC=6，

    ∴OA=3，OP=6，∴∠AOP=60°，

    ∴∠ACP=30°，

    故答案为：30°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-2 1.2二阶矩阵与平面向量的乘法（解析版） 题型：填空题

    （2014•浦东新区二模）函数f（x）=的最大值为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷（解析版） 题型：选择题

    将直线y=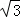x绕原点逆时针旋转60°，所得到的直线为（ ）

    A.x=0 B.y=0 C.y=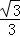x D.y=﹣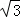x

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 3.2平面与圆柱面的截线练习卷（解析版） 题型：填空题

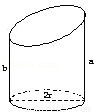
    （2003•北京）如图，已知底面半径为r的圆柱被一个平面所截，剩下部分母线长的最大值为a，最小值为b，那么圆柱被截后剩下部分的体积是 ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 3.1平行射影练习卷（解析版） 题型：填空题

    给出下列四个命题：

    ①设x1，x2∈R，则x1＞1且x2＞1的充要条件是x1+x2＞2且x1x2＞1；

    ②任意的锐角三角形ABC中，有sinA＞cosB成立；

    ③平面上n个圆最多将平面分成2n2﹣4n+4个部分；

    ④空间中直角在一个平面上的正投影可以是钝角．

    其中真命题的序号是 （要求写出所有真命题的序号）．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：填空题

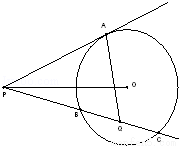
    （2014•陕西二模）如图，已知PA是⊙O的切线，A为切点．PC是⊙O的一条割线，交⊙O于B，C两点，点Q是弦BC的中点．若圆心O在∠APB内部，则∠OPQ+∠PAQ的度数为 ．

     

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷（解析版） 题型：选择题

    如图，经过⊙O上的点 A的切线和弦 BC的延长线相交于点 P，若∠CAP=40°，∠ACP=100°，则

    ∠BAC所对的弧的度数为（ ）

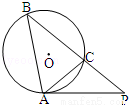
    A.40° B.100° C.120° D.30°

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-1 2.1圆周角定理练习卷（解析版） 题型：选择题

    （2010•海门市模拟）如图，已知∠DEC=80°，弧CD的度数与弧AB的度数的差为20°，则∠DAC的度数为 ．

     

     

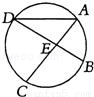
    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年北师大版选修1-2 3.3综合法与分析法练习卷（解析版） 题型：选择题

    （2014•合肥一模）对于函数f（x），若?a，b，c∈R，f（a），f（b），f（c）都是某一三角形的三边长，则称f（x）为“可构造三角形函数”．以下说法正确的是（ ）

    A.f（x）=1（x∈R）不是“可构造三角形函数”

    B.“可构造三角形函数”一定是单调函数

    C.f（x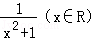）=是“可构造三角形函数”

    D.若定义在R上的函数f（x）的值域是（e为自然对数的底数），则f（x）一定是“可构造三角形函数”

     

    查看答案和解析>>

    同步练习册答案