
 如图所示,已知圆O的半径长为4,两条弦AC,BD相交于点E,若$BD=4\sqrt{3}$,BE>DE,E为AC的中点,$AB=\sqrt{2}AE$.
如图所示,已知圆O的半径长为4,两条弦AC,BD相交于点E,若$BD=4\sqrt{3}$,BE>DE,E为AC的中点,$AB=\sqrt{2}AE$.分析 (1)由已知可证△ABE∽△ACB,即可得到∠ABE=∠ACB,又∠ACD=∠ABE,从而证明∠ACD=∠ACB,得到结论.
(2)连接OA,则OA⊥BD,设垂足为点F,则点F为弦BD的中点,连接OB,可求cos∠AOB=$\frac{OF}{OB}$的值,进而可求∠AOB,及∠ADB的度数.
解答 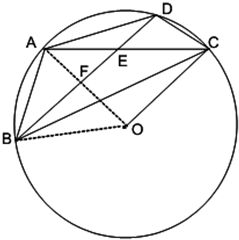 解:(1)由E为AC的中点,$AB=\sqrt{2}AE$,得$\frac{AB}{AE}=\sqrt{2}=\frac{AC}{AB}$.
解:(1)由E为AC的中点,$AB=\sqrt{2}AE$,得$\frac{AB}{AE}=\sqrt{2}=\frac{AC}{AB}$.
又∠BAE=∠CAB,
∴△ABE∽△ACB,
∴∠ABE=∠ACB,
又∠ACD=∠ABE,
∴∠ACD=∠ACB,
故AC平分∠BCD.
(2)连接OA,由点A是弧BAD的中点,则OA⊥BD,
设垂足为点F,则点F为弦BD的中点,$BF=2\sqrt{3}$,
连接OB,则$OF=\sqrt{O{B^2}-B{F^2}}=\sqrt{{4^2}-{{(2\sqrt{3})}^2}}=2$,
∴$cos∠AOB=\frac{OF}{OB}=\frac{2}{4}=\frac{1}{2}$,∠AOB=60°.
∴$∠ADB=\frac{1}{2}∠AOB={30}$°.
点评 本题主要考查了相似三角形的判定及性质,考查了数形结合思想和推理论证能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC一A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
如图,在三棱柱ABC一A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
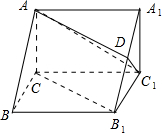 如图在三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,D是A1B1的中点,侧棱CC1⊥底面ABC
如图在三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,D是A1B1的中点,侧棱CC1⊥底面ABC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com