Question

15．已知圆C：x²+y²-6x-2y-6=0，其中C为圆心．
（I）若过点P（1，0）的直线l与圆C交于M、N两点，且$\overrightarrow{CM}$•$\overrightarrow{CN}$=-8，求直线l的方程；
（II）过点P（1，0）作圆C的两条弦BD、EF使得$\overrightarrow{BD}$•$\overrightarrow{EF}$=0，求四边形BEDF面积的最大值．

Answer 1

分析 （Ⅰ）化圆的方程为标准式，求出圆心坐标和半径，验证直线斜率不存在时成立，当直线斜率存在时，设出直线方程，把数量积转化为圆心到直线的距离，代入点到直线的距离公式求得k值，则答案可求；
（Ⅱ）设圆心到BD、EF的距离分别为d₁、d₂，则 d₁²+d₂²=5，代入面积公式S=$\frac{1}{2}$BD•EF，使用基本不等式求出四边形BEDF的面积的最大值．

解答 解：（Ⅰ）化圆C：x²+y²-6x-2y-6=0为（x-3）²+（y-1）²=16，
可得圆C的圆心坐标为C（3，1），半径为4，如图，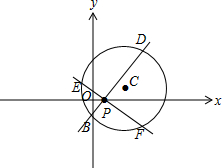

当直线l的斜率不存在时，直线方程为x=1，得M（1，1-$2\sqrt{3}$），N（1，1+$2\sqrt{3}$），
$\overrightarrow{CM}=（-2，-2\sqrt{3}）$，$\overrightarrow{CN}=（-2，2\sqrt{3}）$，$\overrightarrow{CM}$•$\overrightarrow{CN}$=-8，符合题意；
当直线l的斜率存在时，设斜率为k，直线l的方程为y=k（x-1），
由$\overrightarrow{CM}$•$\overrightarrow{CN}$=-8，得$|\overrightarrow{CM}||\overrightarrow{CN}|•cos∠MCN={r}^{2}cos∠MCN=-8$，
即$cos∠MCN=-\frac{1}{2}$，∴∠MCN=120°，
∴圆心C到直线l的距离为d=rsin30°=4×$\frac{1}{2}=2$．
则$\frac{|3k-1-k|}{\sqrt{{k}^{2}+1}}=2$，解得：k=-$\frac{3}{4}$．
∴直线l的方程为y=$\frac{3}{4}（x-1）$，即3x-4y-3=0．
综上，所求直线l的方程为：x=1和3x-4y-3=0；
（Ⅱ）设圆心C到BD、EF的距离分别为d₁、d₂，则d₁²+d₂²=CP²=5．
四边形BEDF的面积为：
S=$\frac{1}{2}$×|BD||EF|=$\frac{1}{2}$×2$\sqrt{16-{{d}_{1}}^{2}}$×$2\sqrt{16-{{d}_{2}}^{2}}$
=2$\sqrt{16-{{d}_{1}}^{2}}\sqrt{16-{{d}_{2}}^{2}}$≤32-（d₁²+d₂²）=27．
当且仅当d₁²=d₂²时取等号．

点评 本题考查平面向量的数量积运算，考查垂径定理及勾股定理的应用，把平面向量数量积转化为圆心到直线距离是解答该题的关键，是中档题．