
分析 先将圆的方程化为标准式,求出圆心和半径,通过分析可以看出,圆心在一条直线m上,半径是定值3,所以直线l∥m,才能满足截得的弦长是定值.
解答 解:将圆C:x2+y2-(6-2m)x-4my+5m2-6m=0化为标准式得
[x-(3-m)]2+(y-2m)2=9,
∴圆心C(3-m,2m),半径r=3,
令$\left\{\begin{array}{l}{x=3-m}\\{y=2m}\end{array}\right.$,消去m得2x+y-6=0,
所以圆心在直线2x+y-6=0上,
又∵直线l经过点(1,-1),
若对任意的实数m,直线l被圆C截得的弦长都是定值,
∴直线l与圆心所在直线平行,
∴设l方程为2x+y+C=0,将(1,-1)代入得C=-1,
∴直线l的方程为2x+y-1=0.
故答案为:2x+y-1=0.
点评 有关直线与圆的位置关系的问题,一般采用几何法,即先求出圆心与半径,然后画出图象,利用点到圆心的距离,半径,弦长等的关系解决问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
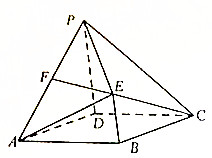 如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点.
如图,四边形ABCD是菱形,PD⊥平面ABCD,PD∥BE,AD=PD=2BE=2,∠DAB=60°,点F为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
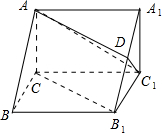 如图在三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,D是A1B1的中点,侧棱CC1⊥底面ABC
如图在三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,D是A1B1的中点,侧棱CC1⊥底面ABC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com