分析:(I)取B
1C
1的中点G,连接EG,GB,过C作CH⊥GB于H,证明AB⊥平面BB
1C
1C,可得AB⊥BC;
(II)取AB中点D,连接ED,DF,证明FC
1∥ED,可得FC
1∥平面ABE
(III)建立空间直角坐标系,求出平面ABE的法向量
=(
,0,-1),平面EFC
1的法向量取
=(
,1,-1),利用向量的夹角公式,即可求平面ABE与平面EFC
1所成锐二面角的余弦值.
解答:(I)证明:取B
1C
1的中点G,连接EG,GB,
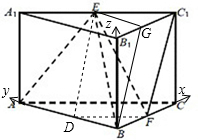
则EG∥AB,GB是平面ABE与平面BB
1C
1C的交线
过C作CH⊥GB于H,则∵平面ABE⊥平面BB
1C
1C
∴CH⊥平面ABE,∴CH⊥AB
∵CC
1⊥AB,CC
1∩CH=C
∴AB⊥平面BB
1C
1C
∵BC?平面BB
1C
1C
∴AB⊥BC
(II)证明:取AB中点D,连接ED,DF,则DF∥EC
1,且DF=EC
1,
∴FC
1∥ED
∵FC
1?平面ABE,ED?平面ABE
∴FC
1∥平面ABE
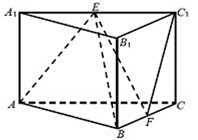
(III)解:∵AB⊥BC,∴AB=2
建立如图所示的坐标系,则B(0,0,0),A(0,2
,0),E(1,
,
),F(1,0,0),C
1(2,0,
)
∴
=(0,2
,0),
=(1,
,
),
=(1,-
,0),
=(1,0,)设
=(x,y,z)是平面ABE的法向量,则
,即
,可取
=(
,0,-1);
设
=(x′,y′,z′)是平面EFC
1的法向量,则
,即
,可取
=(
,1,-1)
∴平面ABE与平面EFC
1所成锐二面角的余弦值为
||=
=
点评:本题考查线面垂直,考查线面平行,考查面面角,考查向量知识的运用,解题的关键是掌握线面垂直、线面平行的判定方法,正确求出平面的法向量.

 在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=
在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=


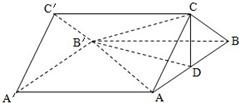 如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点.
如图,在直三棱柱ABC-A′B′C′中,已知AA′=4,AC=BC=2,∠ACB=90°,D是AB的中点. 如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数).
如图,在直三棱柱ABC-A′B′C′中,AA′=AB=BC=1,∠ABC=90°.棱A′C′上有两个动点E,F,且EF=a (a为常数). 如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角.
如图所示,在直三棱柱ABC-A′B′C′中,∠BAC=90°,AB=BB′=1,直线B′C与平面ABC成30°角. 如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,
如图,在直三棱柱ABC-A′B′C′中,点D是BC的中点,∠ACB=90°,AC=BC=1,AA′=2,