
分析 (1)由题意可知:求得c,利用等差数列性质及椭圆的离心率公式,即可求得a和b的值,求得椭圆方程;
(2)分类,当$α≠\frac{π}{2}$时,由α+β=π,知$β≠\frac{π}{2}$,且这两条直线的斜率互为相反数,设直线方程,代入椭圆方程,利用韦达定理及弦长公式即可求得丨AB丨,丨DE丨,即可求得$\frac{{{{|{AB}|}^2}}}{{|{DE}|}}$的值;
①当$α=\frac{π}{2}$时,由α+β=π,知$β=\frac{π}{2}$,则l1:x=0,l2:x=-1,求得丨AB丨,丨DE丨,求得$\frac{{{{|{AB}|}^2}}}{{|{DE}|}}$的值.
解答 解:(1)由题可知,椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F1(-1,0),c=1,b2=3ae=3×$\frac{c}{a}$×a=3c,
a2=b2+c2,解得$\left\{{\begin{array}{l}{{b^2}=3}\\{{a^2}=4}\end{array}}\right.$,
所以椭圆的方程是$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(2)设倾斜角为α的直线为l1,倾斜角为β的直线l2,
①当$α=\frac{π}{2}$时,由α+β=π,知$β=\frac{π}{2}$,则l1:x=0,l2:x=-1,
于是$|{AB}|=2b=2\sqrt{3},|{DE}|=\frac{{2{b^2}}}{a}=3$,此时$\frac{{{{|{AB}|}^2}}}{{|{DE}|}}=4$;
②当$α≠\frac{π}{2}$时,由α+β=π,知$β≠\frac{π}{2}$,且这两条直线的斜率互为相反数,
设l1:y=kx,则l2:y=-k(x+1),
由$\left\{{\begin{array}{l}{y=kx}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$,可得$\left\{{\begin{array}{l}{{x^2}=\frac{12}{{4{k^2}+3}}}\\{{y^2}=\frac{{12{k^2}}}{{4{k^2}+3}}}\end{array}}\right.$,
则${|{AB}|^2}={({2\sqrt{{x^2}+{y^2}}})^2}=4({\frac{{12+12{k^2}}}{{4{k^2}+3}}})=\frac{{48({{k^2}+1})}}{{4{k^2}+3}}$,
由$\left\{{\begin{array}{l}{y=-kx-k}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$可得:(4k2+3)x2+8k2x+4k2-12=0,
由于△=(8k)2-4(4k2+3)(4k2-12)=4(36k2+36)>0,
设l2与椭圆的两个交点坐标依次为D(x1,y1),E(x2,y2),
于是${x_1}+{x_2}=-\frac{{8{k^2}}}{{4{k^2}+3}},{x_1}{x_2}=\frac{{4{k^2}-12}}{{4{k^2}+3}}$,
∴$|{DE}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\sqrt{1+{k^2}}\sqrt{{{({{x_1}+{x_2}})}^2}-4{x_1}{x_2}}$
=$\sqrt{1+{k}^{2}}$•$\sqrt{(-\frac{8{k}^{2}}{4{k}^{2}+3})^{2}-4(\frac{4{k}^{2}-12}{4{k}^{2}+3})}$,
=$\frac{12({k}^{2}+1)}{4{k}^{2}+3}$
$\frac{{{{|{AB}|}^2}}}{{|{DE}|}}=\frac{{\frac{{48({{k^2}+1})}}{{4{k^2}+3}}}}{{\frac{{12({{k^2}+1})}}{{4{k^2}+3}}}}=4$,
综上所述总有$\frac{{{{|{AB}|}^2}}}{{|{DE}|}}=4$.
点评 本题考查椭圆的简单几何性质,直线与椭圆的位置关系,韦达定理,弦长公式,考查计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
 如图,在边长是2的正方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点.
如图,在边长是2的正方体ABCD-A1B1C1D1中,E,F分别为AB,A1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,1]∪\left\{{\frac{3}{2}}\right\}$ | B. | $(0,\frac{3}{2}]$ | C. | $(0,1)∪\left\{{\frac{3}{2}}\right\}$ | D. | $(0,\frac{3}{2})∪\left\{0\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
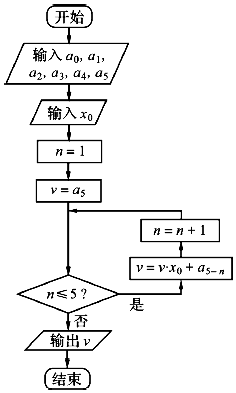 执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )
执行如图所示的程序框图,若输入a0=0,a1=1,a2=2,a3=3,a4=4,a5=5,x0=-1,则输出v的值为( )| A. | 15 | B. | 3 | C. | -3 | D. | -15 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈R,λ>0),
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}$=λ$\overrightarrow{AF}$(λ∈R,λ>0),查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-2) | B. | [-3,-2] | C. | (-∞,-3)∪(-2,+∞) | D. | (-∞,-3)∪[-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
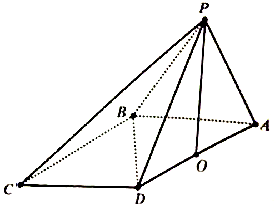 在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.
在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AB⊥平面BB1C1C,且四边形BB1C1C是菱形,∠BCC1=60°.
如图,在三棱柱ABC-A1B1C1中,AB⊥平面BB1C1C,且四边形BB1C1C是菱形,∠BCC1=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com