
分析 求出$\overrightarrow{a},\overrightarrow{b}$的夹角,求出$\overrightarrow{a},\overrightarrow{b}$的终点坐标,设$\overrightarrow{c}$的终点坐标为(x,y),利用向量垂直得出C的轨迹方程,转化为平面几何中的距离问题.
解答 解:∵|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=$\overrightarrow{a}•\overrightarrow{b}$=3,∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{\sqrt{2}}{2}$.∴$\overrightarrow{a},\overrightarrow{b}$的夹角为45°.
设$\overrightarrow{OA}=\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,O为坐标原点.则|$\overrightarrow{b}-\overrightarrow{c}$|=|BC|.
设A($\sqrt{2}$,0),B($\frac{3\sqrt{2}}{2}$,$\frac{3\sqrt{2}}{2}$),设C(x,y),
则$\overrightarrow{c}-2\overrightarrow{a}$=(x-2$\sqrt{2}$,y),2$\overrightarrow{b}-3\overrightarrow{c}$=(3$\sqrt{2}$-3x,3$\sqrt{2}$-3y),
∵($\overrightarrow{c}-2\overrightarrow{a}$)•(2$\overrightarrow{b}-3\overrightarrow{c}$)=0,∴(x-2$\sqrt{2}$)(3$\sqrt{2}$-3x)+y(3$\sqrt{2}$-3y)=0,
整理得:x2+y2-3$\sqrt{2}$x-$\sqrt{2}$y+4=0,即(x-$\frac{3\sqrt{2}}{2}$)2+(y-$\frac{\sqrt{2}}{2}$)2=1.
∴点C的轨迹为以M($\frac{3\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)为圆心,以r=1为半径的圆.
∴点B到圆心M的距离d=$\sqrt{2}$,
∴BC的最大距离为d+r=$\sqrt{2}+1$.即|$\overrightarrow{b}-\overrightarrow{c}$|的最大值为$\sqrt{2}+1$.
故答案为$\sqrt{2}+1$.
点评 本题考查了平面向量运算的几何意义,使用坐标法计算是常用解题方法.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}或2$ | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}或5$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{14}-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{14}+\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
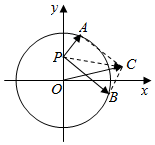 如图,已知点P(0,$\frac{\sqrt{2}}{3}$),点A,B是单位圆O上的两个动点,若$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,动点C满足$\overrightarrow{PC}$=$\overrightarrow{PA}+\overrightarrow{PB}$,则关于|$\overrightarrow{OC}$|的说法正确的是( )
如图,已知点P(0,$\frac{\sqrt{2}}{3}$),点A,B是单位圆O上的两个动点,若$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,动点C满足$\overrightarrow{PC}$=$\overrightarrow{PA}+\overrightarrow{PB}$,则关于|$\overrightarrow{OC}$|的说法正确的是( )| A. | |$\overrightarrow{OC}$|随点A,B位置的改变而变化,且最大值为$\frac{4}{3}$ | |
| B. | |$\overrightarrow{OC}$|随点A,B位置的改变而变化,且最小值为$\frac{4}{3}$ | |
| C. | |$\overrightarrow{OC}$|是一个常数,且值为$\frac{4}{3}$ | |
| D. | 以上说法都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{25}{16}$ | C. | $\frac{121}{16}$ | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com