Question

10．已知直三棱柱ABC-A₁B₁C₁中，AB=3，BC=AA₁=2，∠ABC=$\frac{π}{3}$，则异面直线B₁A与C₁B所成角的余弦值为（　　）

• A． $\frac{\sqrt{13}}{13}$
• B． $\frac{\sqrt{13}}{26}$
• C． $\frac{\sqrt{13}}{52}$
• D． $\frac{\sqrt{26}}{52}$

Answer 1

分析 连接B₁C交BC₁于E，连接DE，利用四边形BCC₁B₁是平行四边形及其三角形的中位线定理证明DE∥AB₁，可得∠DEB或其补角为异面直线AB₁与BC₁所成的角，再利用余弦定理即可得出．

解答 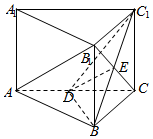解：如图所示，取AC中点D，连接B₁C交BC₁于E，连接DE，
∵四边形BCC₁B₁是平行四边形，∴B₁E=EC．
又AD=DC．∴DE∥AB₁，
∴∠DEB或其补角为异面直线AB₁与BC₁所成的角，
DE=$\frac{1}{2}A{B}_{1}$=$\frac{\sqrt{{3}^{2}+{2}^{2}}}{2}=\frac{\sqrt{13}}{2}$，
∵$\overrightarrow{BD}=\frac{1}{2}（\overrightarrow{BA}+\overrightarrow{BC}）$，∴${\overrightarrow{BD}}^{2}=\frac{1}{4}（{\overrightarrow{BA}}^{2}+{\overrightarrow{BC}}^{2}+2\overrightarrow{BA}•\overrightarrow{BC}）$，∴DB=$\frac{\sqrt{19}}{2}$，
BE=$\frac{1}{2}B{C}_{1}=\sqrt{2}$
在△DEB中，由余弦定理得DB²=BE²+DE²-2BE•DEcos∠DEB，
$\frac{19}{4}$=$\frac{13}{4}$+2-2×$\frac{\sqrt{13}}{2}×\sqrt{2}$×cos∠DEB，解得cos∠DEB=$\frac{\sqrt{26}}{52}$；
∴则异面直线B₁A与C₁B所成角的余弦值为$\frac{\sqrt{26}}{52}$．
故选：D．

点评 本题考查了空间中的两条异面直线所成角的计算问题，也考查了空间中的平行关系应用问题，是中档题．