
【题目】已知点P(1,1),过点P动直线l与圆C:x2+y2﹣2y﹣4=0交与点A,B两点.
(1)若|AB|= ![]() ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)求线段AB中点M的轨迹方程.
【答案】
(1)解:由题意:圆C:x2+y2﹣2y﹣4=0,
化为圆的标准方程x2+(y﹣1)2=5,圆心C(0,1),r= ![]() .
.
∵又|AB|= ![]()
当动直线l的斜率不存在时,直线l的方程为x=1时,显然不满足题意;
当动直线l的斜率存在时,设动直线l的方程为:y﹣1=k(x﹣1)即kx﹣y+1﹣k=0
故弦心距d= ![]() =
= ![]() .
.
再由点到直线的距离公式可得d= ![]() =
= ![]() ,
,
解得:k=± ![]() .
.
即直线l的斜率等于± ![]() ,
,
根据tanθ=k,
故得直线l的倾斜角等于 ![]() 或
或 ![]() .
.
(2)解:由题意:线段AB中点为M,设M的坐标(x,y),
由垂径定理可知∠PMC=90°,故点M的轨迹是以CP为直径的圆,
又∵点C(0,1),P(1,1)
故M的轨迹方程为 ![]() .
.
【解析】(1)利用点斜式,设出过P点的直线l,利用与圆的弦长为 ![]() ,求出k的值,可得直线l的倾斜角;(2)设M的坐标(x,y),由垂径定理可知∠PMC=90°,故点M的轨迹是以CP为直径的圆.可得方程.
,求出k的值,可得直线l的倾斜角;(2)设M的坐标(x,y),由垂径定理可知∠PMC=90°,故点M的轨迹是以CP为直径的圆.可得方程.


科目:高中数学 来源: 题型:
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
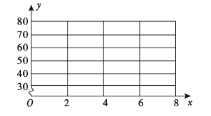
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式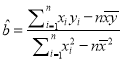 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿海准备购买“海马”牌一辆小汽车,其中购车费用12.8万元,每年的保险费、汽油费约为0.95万元,年维修、保养费第一年是0.1万元,以后逐年递增0.1万元.请你帮阿海计算一下这种汽车使用多少年,它的年平均费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了了解高二年级学生对教师教学的意见,打算从高二年级883名学生中抽取80名进行座谈,若采用下面的方法选取:先用简单随机抽样从883人中剔除3人,剩下880人再按系统抽样的方法进行,则每人入选的概率是( )
A.![]()
B.![]()
C.![]()
D.无法确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求证: 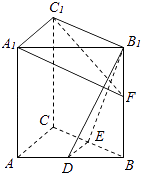
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(k)是满足不等式log2x+log2(52k﹣1﹣x)≥2k(k∈N*)的自然数x的个数.
(1)求f(k)的函数解析式;
(2)Sn=f(1)+2f(2)+…+nf(n),求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,关于实数
,关于实数![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的不等式:
的不等式: ![]() ;
;
(2)是否存在实数![]() ,使得关于
,使得关于![]() 的函数
的函数![]() (
(![]() )的最小值为
)的最小值为![]() ?若存在,求实数
?若存在,求实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com