
分析 (1)由复数模长的几何意义和线段的垂直平分线可得x+2y=3,由基本不等式可得;
(2)由复数模长的几何意义$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,三角换元可得x=2cosθ,y=$\sqrt{3}$sinθ,由复数的模长公式和三角函数可得.
解答 解:(1)∵z满足|z-4i|=|z+2|,
∴z=x+yi表示到(0,4)和(-2,0)距离相等的点,
由线段的垂直平分线可得x+2y=3,
故2x+4y≥2$\sqrt{{2}^{x}•{4}^{y}}$=2$\sqrt{{2}^{x+2y}}$=4$\sqrt{2}$,
当且仅当2x=4y即x=$\frac{3}{2}$且y=$\frac{3}{4}$时取等号
故2x+4y的最小值为4$\sqrt{2}$,相应x、y值分别为$\frac{3}{2}$和$\frac{3}{4}$;
(2)∵z满足|z-1|+|z+1|=4.
∴z在以(-1,0)和(1,0)为焦点的椭圆上
可得椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,
故可得x=2cosθ,y=$\sqrt{3}$sinθ
∴|z|2=4cos2θ+3sin2θ=3+cos2θ∈[3,4],
∴|z|的取值范围为[$\sqrt{3}$,2]
点评 本题考查复数求模,涉及基本不等式和三角换元的思想,属中档题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{3}$ | C. | 3 | D. | -1或$\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
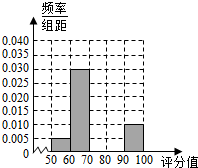 某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.
某地有2000名学生参加数学学业水平考试,现将成绩(满分:100分)汇总,得到如图所示的频率分布表.| 成绩分组 | 频数 | 频率 |
| [50,60] | 100 | |
| (60,70] | ||
| (70,80] | 800 | |
| (80,90] | ||
| (90,100] | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | -3 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com