
分析 画出满足条件的平面区域,求出角点的坐标,得到$\overrightarrow{OM}$•$\overrightarrow{ON}$的表达式,通过平移直线求出其最大值即可.
解答 解:画出满足条件的平面区域,如图示: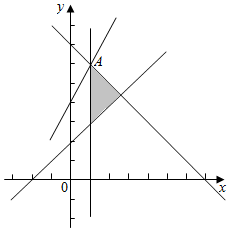 ,
,
由$\left\{\begin{array}{l}{x=1}\\{x+y=7}\end{array}\right.$,解得:A(1,6),
设M(x,y),则$\overrightarrow{OM}$•$\overrightarrow{ON}$=-2x+y,
令-2x+y=z,则y=2x+z,
平移直线发现y=2x+z过A(1,6)时,z最大,
z的最大值是:z=-2+6=4,
故答案为:4.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
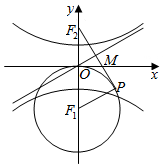 如图,已知F1,F2是双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的上下焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为2.
如图,已知F1,F2是双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的上下焦点,过F2点作以F1为圆心,|OF1|为半径的圆的切线,P为切点,若切线段PF2被一条渐近线平分,则双曲线的离心率为2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{10}$,10] | B. | ($\frac{1}{10}$,10) | C. | [$\frac{1}{10}$,1)∪(1,10] | D. | ($\frac{1}{10}$,10] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com