
分析 利用二项式展开式的通项公式,令x的指数为4,求出r的值,即可得出展开式中x4的系数.
解答 解:${(x-\frac{1}{{\root{3}{x}}})^8}$展开式的通项公式为:
Tr+1=${C}_{8}^{r}$•x8-r•${(-\frac{1}{\root{3}{x}})}^{r}$=(-1)r•${C}_{8}^{r}$•${x}^{8-\frac{4r}{3}}$,
令8-$\frac{4r}{3}$=4,解得r=3;
∴展开式中x4的系数为:
(-1)3•${C}_{8}^{3}$=-56.
故答案为:-56.
点评 本题考查了利用二项式展开式的通项公式求某一项的系数问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3}{4}<p≤\frac{7}{8}$ | B. | $p>\frac{5}{16}$ | C. | $\frac{7}{8}≤p<\frac{5}{16}$ | D. | $\frac{7}{8}<p≤\frac{5}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$i | B. | $\frac{1}{2}$i | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
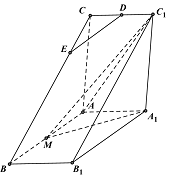 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com