
| A. | 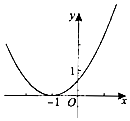 | B. | 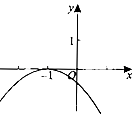 | ||
| C. | 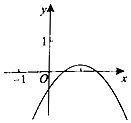 | D. | 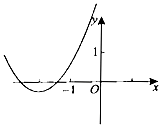 |
分析 先求出函数f(x)ex的导函数,利用x=-1为函数f(x)ex的一个极值点可得a,b,c之间的关系,再代入函数f(x)=ax2+bx+c,对答案分别代入验证,看哪个答案不成立即可.
解答 解:由y=f(x)ex=ex(ax2+bx+c)⇒y′=f′(x)ex+exf(x)=ex[ax2+(b+2a)x+b+c],
由x=-1为函数f(x)ex的一个极值点可得,-1是方程ax2+(b+2a)x+b+c=0的一个根,
所以有a-(b+2a)+b+c=0⇒c=a.
法一:所以函数f(x)=ax2+bx+a,对称轴为x=-$\frac{b}{2a}$,且f(-1)=2a-b,f(0)=a.
对于A,由图得a>0,f(0)>0,f(-1)=0,不矛盾,
对于B,由图得a<0,f(0)<0,f(-1)=0,不矛盾,
对于C,由图得a<0,f(0)<0,x=-$\frac{b}{2a}$>0⇒b>0⇒f(-1)<0,不矛盾,
对于D,由图得a>0,f(0)>0,x=-$\frac{b}{2a}$<-1⇒b>2a⇒f(-1)<0与原图中f(-1)>0矛盾,D不对.
法二:所以函数f(x)=ax2+bx+a,由此得函数相应方程的两根之积为1,对照四个选项发现,D不成立.
故选:D.
点评 本题考查极值点与导函数之间的关系.一般在知道一个函数的极值点时,直接把极值点代入导数令其等0即可.可导函数的极值点一定是导数为0的点,但导数为0的点不一定是极值点.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
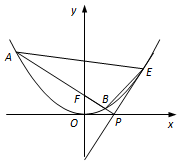 在平面直角坐标系xOy中,已知抛物线x2=2py(p>0)上的点M(m,1)到焦点F的距离为2,
在平面直角坐标系xOy中,已知抛物线x2=2py(p>0)上的点M(m,1)到焦点F的距离为2,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>a>c | C. | a>b>c | D. | c>b>a |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com