
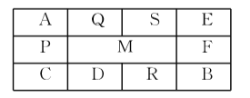
【题目】图是一个![]() 的方格(其中心的方格线已被划去).一只青蛙停在
的方格(其中心的方格线已被划去).一只青蛙停在![]() 格处,从某一时刻起,青蛙每隔一秒钟就跳到与它所在方格有公共边的另一方格内,直至跳到
格处,从某一时刻起,青蛙每隔一秒钟就跳到与它所在方格有公共边的另一方格内,直至跳到![]() 格才停下..若青蛙经过每一个方格不超过一次,则青蛙的跳法总数为________.
格才停下..若青蛙经过每一个方格不超过一次,则青蛙的跳法总数为________.

【答案】26
【解析】
如图,分两种情况讨论.
(1)如果青蛙不经过![]() 格,则有2条路径:
格,则有2条路径:![]() ,
,![]() .
.
(2)如果青蛙经过![]() 格,若某时刻青蛙跳到
格,若某时刻青蛙跳到![]() 格,则它下一秒内一定跳至
格,则它下一秒内一定跳至![]() 格;若某时刻青蛙跳到
格;若某时刻青蛙跳到![]() 格,则它下一秒内一定不会跳至
格,则它下一秒内一定不会跳至![]() 格.因此,可将
格.因此,可将![]() 、
、![]() 两格合并为一个大方格(设之为
两格合并为一个大方格(设之为![]() ).同样地,可将
).同样地,可将![]() 、
、![]() 两格合并为大方格
两格合并为大方格![]() .
.
如果两个方格有公共边,则在两个方格间连上虚线,如图9.
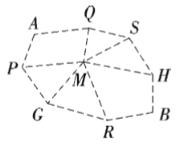
由图可知,![]() 、
、![]() 、
、![]() 和
和![]() 、
、![]() 、
、![]() 对称地分布在直线
对称地分布在直线![]() 的两侧.
的两侧.
显然,青蛙第一步必跳入![]() 、
、![]() 两格中的某格,倒数第二步必跳入
两格中的某格,倒数第二步必跳入![]() 、
、![]() 两格中的某格.
两格中的某格.
如果青蛙第一步跳至![]() 格,倒数第二步跳至
格,倒数第二步跳至![]() 格,那么,这样的路径有3条:
格,那么,这样的路径有3条:![]() ,
,![]() ,
,![]() .
.
如果青蛙第一步跳至![]() 格,倒数第二步跳至
格,倒数第二步跳至![]() 格,设青蛙第
格,设青蛙第![]() 秒钟跳至
秒钟跳至![]() 格,第
格,第![]() 秒跳至
秒跳至![]() 格,第
格,第![]() 秒跳至
秒跳至![]() 格.
格.
则![]() 格可以是
格可以是![]() 、
、![]() 、
、![]() 、
、![]() 格可以是
格可以是![]() 、
、![]() 、
、![]() .因此,这样的路径有
.因此,这样的路径有![]() 条.
条.
由对称性知,如果青蛙第一步跳至![]() 格,倒数第二步跳至
格,倒数第二步跳至![]() 格,则这样的路径有3条;如果青蛙第一步跳
格,则这样的路径有3条;如果青蛙第一步跳![]() 格,倒数第二步跳至
格,倒数第二步跳至![]() 格,则这样的路径有9条.
格,则这样的路径有9条.
综上,青蛙的跳法总数为![]() .
.


科目:高中数学 来源: 题型:
【题目】某单位从一所学校招收某类特殊人才.对![]() 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
| 一般 | 良好 | 优秀 |
一般 |
|
|
|
良好 |
|
|
|
优秀 |
|
|
|
例如表中运动协调能力良好且逻辑思维能力一般的学生是![]() 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这![]() 位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到逻辑思维能力优秀的学生的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)从运动协调能力为优秀的学生中任意抽取![]() 位,求其中至少有一位逻辑思维能力优秀的学生的概率.
位,求其中至少有一位逻辑思维能力优秀的学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某年数学竞赛请自以为来自X星球的选手参加填空题比赛,共10道题目,这位选手做题有一个古怪的习惯:先从最后一题(第10题)开始往前看,凡是遇到会的题就作答,遇到不会的题目先跳过(允许跳过所有的题目),一直看到第1题;然后从第1题开始往后看,凡是遇到先前未答的题目就随便写个答案,遇到先前已答的题目则跳过(例如,他可以按照9,8,7,4,3,2,1,5,6,10的次序答题),这样所有的题目均有作答,设这位选手可能的答题次序有n种,则n的值为( )
A.512B.511C.1024D.1023
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设锐角![]() 的外接圆的半径为
的外接圆的半径为![]() ,在
,在![]() 内取外接圆的同心圆
内取外接圆的同心圆![]() ,其半径为
,其半径为![]()
![]() ,从圆
,从圆![]() 上任取一点
上任取一点![]() ,作
,作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
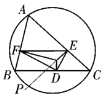
(1)求证:![]() 的面积为定值;
的面积为定值;
(2)猜想:当![]() 为任意三角形、同心圆
为任意三角形、同心圆![]() 为任意同心圆时,结论是否成立(不要求证明)?
为任意同心圆时,结论是否成立(不要求证明)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难度的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题,测试前根据对学生的了解,预估了每道题的难度,如表所示:
为参加测试的总人数.现对某校高三年级240名学生进行一次测试,共5道客观题,测试前根据对学生的了解,预估了每道题的难度,如表所示:
题号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度 | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
测试后,从中随机抽取了20名学生的答题数据进行统计,结果如表:

(Ⅰ)根据题中数据,估计中240名学生中第5题的实测答对人数;
(Ⅱ)从抽样的20名学生中随机抽取2名学生,记这2名学生中第5题答对的人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)试题的预估难度和实测难度之间会有偏差.设![]() 为第
为第![]() 题的实测难度,请用
题的实测难度,请用![]() 和
和![]() 设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.
设计一个统计量,并制定一个标准来判断本次测试对难度的预估是否合理.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】田忌赛马是![]() 史记
史记![]() 中记载的一个故事,说的是齐国将军田忌经常与齐国众公子赛马,孙膑发也们的马脚力都差不多,都分为上、中、下三等
中记载的一个故事,说的是齐国将军田忌经常与齐国众公子赛马,孙膑发也们的马脚力都差不多,都分为上、中、下三等![]() 于是孙膑给田忌将军制定了一个必胜策略:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得公子们许多赌注
于是孙膑给田忌将军制定了一个必胜策略:比赛即将开始时,他让田忌用下等马对战公子们的上等马,用上等马对战公子们的中等马,用中等马对战公子们的下等马,从而使田忌赢得公子们许多赌注![]() 假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示:
假设田忌的各等级马与某公子的各等级马进行一场比赛获胜的概率如表所示:
田忌的马 | 上等马 | 中等马 | 下等马 |
上等马 |
|
| 1 |
中等马 |
|
|
|
下等马 | 0 |
|
|
比赛规则规定:一次比由三场赛马组成,每场由公子和田忌各出一匹马出骞,结果只有胜和负两种,并且毎一方三场赛马的马的等级各不相同,三场比赛中至少获胜两场的一方为最终胜利者.
![]() 如果按孙膑的策略比赛一次,求田忌获胜的概率;
如果按孙膑的策略比赛一次,求田忌获胜的概率;
![]() 如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
如果比赛约定,只能同等级马对战,每次比赛赌注1000金,即胜利者赢得对方1000金,每月比赛一次,求田忌一年赛马获利的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com