
【题目】如图,直三棱柱ABC﹣A1B1C1中,AC=BC=AA1=3,AC⊥BC,点M在线段AB上.
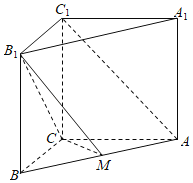
(1)若M是AB中点,证明AC1∥平面B1CM;
(2)当BM![]() 时,求直线C1A1与平面B1MC所成角的正弦值.
时,求直线C1A1与平面B1MC所成角的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连结BC1,交B1C于E,连结ME.利用三角形的中位线证得![]() ,由此证得
,由此证得![]() 平面
平面![]() .
.
(2)以![]() 为原点建立空间直角坐标系,通过直线
为原点建立空间直角坐标系,通过直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,计算出线面角的正弦值.
的法向量,计算出线面角的正弦值.
(1)证明:连结BC1,交B1C于E,连结ME.
∵侧面BB1C1C为矩形,
∴E为BC1的中点,又M是AB的中点,
∴ME∥AC1.
又ME平面B1CM,AC1平面B1CM,
∴AC1∥平面B1CM.
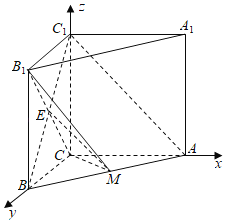
(2)以C为原点,以CB,CA,CC1为坐标轴建立空间直角坐标系C﹣xyz如图所示:
则B1(0,3,3),A1(3,0,3),A(3,0,0),B(0,3,0),C1(0,0,3),AB=3![]() ,∴BM
,∴BM![]() BA.
BA.
∴![]() (0,3,3),
(0,3,3),![]() (1,2,0),
(1,2,0),![]() (3,0,0).
(3,0,0).
设平面B1MC的法向量为![]() (x,y,z),则
(x,y,z),则![]() 0,
0,![]() ,
,
∴![]() ,令z=1得
,令z=1得![]() (2,﹣1,1).
(2,﹣1,1).
∴cos![]() ,
,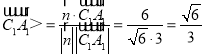 .
.
故当BM![]() 时,直线C1A1与平面B1MC所成角的正弦值为
时,直线C1A1与平面B1MC所成角的正弦值为![]() .
.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位: ![]() )和年利润
)和年利润![]() (单位:千元)的影响,对近8年的年宣传费
(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

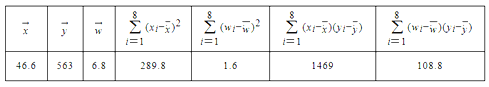
表中![]() ,
,![]() .
.
(1)根据散点图判断, ![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利润![]() 与
与![]() 、
、![]() 的关系为
的关系为![]() .根据(2)的结果要求:年宣传费
.根据(2)的结果要求:年宣传费![]() 为何值时,年利润最大?
为何值时,年利润最大?
附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为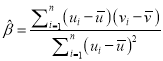 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求线段![]() 的长和
的长和![]() 的积.
的积.
查看答案和解析>>
科目:高中数学 来源: 题型:
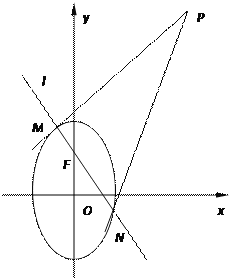
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且上焦点为
,且上焦点为![]() ,过
,过![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点.设点
两点.设点![]() ,记
,记![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 和
和![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)如果直线![]() 的斜率等于
的斜率等于![]() ,求
,求![]() 的值;
的值;
(3)探索![]() 是否为定值?如果是,求出该定值;如果不是,求出
是否为定值?如果是,求出该定值;如果不是,求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lg(﹣x2+5x﹣6)的定义域为A,函数g(x)![]() ,x∈(0,m)的值域为B.
,x∈(0,m)的值域为B.
(1)当m=2时,求A∩B;
(2)若“x∈A”是“x∈B”的必要不充分条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD为矩形,点A、E、B、F共面,且![]() 和
和![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() 90°.
90°.

(Ⅰ)若平面ABCD![]() 平面AEBF,证明平面BCF
平面AEBF,证明平面BCF![]() 平面ADF;
平面ADF;
(Ⅱ)问在线段EC上是否存在一点G,使得BG∥平面CDF,若存在,求出此时三棱锥G-ABE与三棱锥G-ADF的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部门在同一上班高峰时段对甲、乙两座地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟).将统计数据按![]() ,
,![]() ,
,![]() ,
,![]() 分组,制成频率分布直方图:
分组,制成频率分布直方图:

(1)求![]() 的值;
的值;
(2)记![]() 表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”,试估计
表示事件“在上班高峰时段某乘客在甲站乘车等待时间少于20分钟”,试估计![]() 的概率;
的概率;
(3)假设同组中的每个数据用该组区间左端点值来估计,记在上班高峰时段甲、乙两站各抽取的50名乘客乘车的平均等待时间分别为![]() ,
,![]() ,求
,求![]() 的值,并直接写出
的值,并直接写出![]() 与
与![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科技的发展,网购已经逐渐融入了人们的生活.在家里面不用出门就可以买到自己想要的东西,在网上付款即可,两三天就会送到自己的家门口,如果近的话当天买当天就能送到,或者第二天就能送到,所以网购是非常方便的购物方式.某公司组织统计了近五年来该公司网购的人数![]() (单位:人)与时间
(单位:人)与时间![]() (单位:年)的数据,列表如下:
(单位:年)的数据,列表如下:
| 1 | 2 | 3 | 4 | 5 |
| 24 | 27 | 41 | 64 | 79 |
(1)依据表中给出的数据,是否可用线性回归模型拟合![]() 与
与![]() 的关系,请计算相关系数
的关系,请计算相关系数![]() 并加以说明(计算结果精确到0.01).(若
并加以说明(计算结果精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式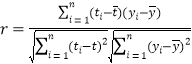
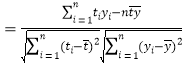 ,参考数据
,参考数据![]() .
.
(2)建立![]() 关于
关于![]() 的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
的回归方程,并预测第六年该公司的网购人数(计算结果精确到整数).
(参考公式: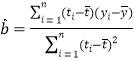
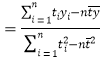 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方形![]() 中,点
中,点![]() ,
,![]() 分别为边
分别为边![]() ,
,![]() 的中点,将
的中点,将![]() 沿
沿![]() 所在直线进行翻折,将
所在直线进行翻折,将![]() 沿
沿![]() 所在直线进行翻折,在翻折的过程中,
所在直线进行翻折,在翻折的过程中,
①点![]() 与点
与点![]() 在某一位置可能重合;②点
在某一位置可能重合;②点![]() 与点
与点![]() 的最大距离为
的最大距离为![]() ;
;
③直线![]() 与直线
与直线![]() 可能垂直; ④直线
可能垂直; ④直线![]() 与直线
与直线![]() 可能垂直.
可能垂直.
以上说法正确的个数为( )
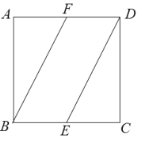
A. 0B. 1C. 2D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com