
ЁОЬтФПЁПФГВПУХдкЭЌвЛЩЯАрИпЗхЪБЖЮЖдМзЁЂввСНзљЕиЬњеОИїЫцЛњГщШЁСЫ50УћГЫПЭЃЌЭГМЦЦфГЫГЕЕШД§ЪБМфЃЈжИГЫПЭДгНјеОПкЕНГЫЩЯГЕЕФЪБМфЃЌГЫГЕЕШД§ЪБМфВЛГЌЙ§40ЗжжгЃЉ.НЋЭГМЦЪ§ОнАД![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЗжзщЃЌжЦГЩЦЕТЪЗжВМжБЗНЭМЃК
ЗжзщЃЌжЦГЩЦЕТЪЗжВМжБЗНЭМЃК

ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉМЧ![]() БэЪОЪТМўЁАдкЩЯАрИпЗхЪБЖЮФГГЫПЭдкМзеОГЫГЕЕШД§ЪБМфЩйгк20ЗжжгЁБЃЌЪдЙРМЦ
БэЪОЪТМўЁАдкЩЯАрИпЗхЪБЖЮФГГЫПЭдкМзеОГЫГЕЕШД§ЪБМфЩйгк20ЗжжгЁБЃЌЪдЙРМЦ![]() ЕФИХТЪЃЛ
ЕФИХТЪЃЛ
ЃЈ3ЃЉМйЩшЭЌзщжаЕФУПИіЪ§ОнгУИУзщЧјМфзѓЖЫЕужЕРДЙРМЦЃЌМЧдкЩЯАрИпЗхЪБЖЮМзЁЂввСНеОИїГщШЁЕФ50УћГЫПЭГЫГЕЕФЦНОљЕШД§ЪБМфЗжБ№ЮЊ![]() ,
,![]() ,Чѓ
,Чѓ![]() ЕФжЕЃЌВЂжБНгаДГі
ЕФжЕЃЌВЂжБНгаДГі![]() гы
гы![]() ЕФДѓаЁЙиЯЕ.
ЕФДѓаЁЙиЯЕ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЦЕТЪЗжВМжБЗНЭМаЁГЄЗНаЮУцЛ§жЎКЭЮЊ1ШЗЖЈaЕФжЕМДПЩЃЛ
ЃЈ2ЃЉгЩЬтвтЃЌРћгУЦЕТЪНќЫЦИХТЪжЕЃЌМЦЫуЪТМўAЕФИХТЪМДПЩЃЛ
ЃЈ3ЃЉНсКЯжБЗНЭМжаЕФЪ§ОнЪзЯШЧѓЕУ![]() ЕФжЕЃЌШЛКѓБШНЯ
ЕФжЕЃЌШЛКѓБШНЯ![]() гы
гы![]() ЕФДѓаЁЙиЯЕМДПЩ.
ЕФДѓаЁЙиЯЕМДПЩ.
ЃЈ1ЃЉвђЮЊ![]() ЃЌ
ЃЌ
Ыљвд![]() .
.
ЃЈ2ЃЉгЩЬтвтжЊЃЌИУГЫПЭдкМзеОЦНОљЕШД§ЪБМфЩйгк20ЗжжгЕФЦЕТЪЮЊЃК
![]() ЃЌЙЪ
ЃЌЙЪ![]() ЕФЙРМЦжЕЮЊ
ЕФЙРМЦжЕЮЊ![]()
ЃЈ3ЃЉ![]()
![]()
![]()
![]()
![]()
![]() .
.
гЩжБЗНЭМжЊЃК![]() .
.


 ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБШ§Ртжљ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕу.
ЕФжаЕу.

ЃЈIЃЉШє![]() ЮЊ
ЮЊ![]() ЩЯЕФвЛЕуЃЌЧв
ЩЯЕФвЛЕуЃЌЧв![]() гыжБЯп
гыжБЯп![]() ДЙжБЃЌЧѓ
ДЙжБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂђЃЉдкЃЈIЃЉЕФЬѕМўЯТЃЌЩшвьУцжБЯп![]() гы
гы![]() ЫљГЩЕФНЧЮЊ45ЁуЃЌЧѓжБЯп
ЫљГЩЕФНЧЮЊ45ЁуЃЌЧѓжБЯп![]() гыЦНУц
гыЦНУц![]() ГЩНЧЕФе§ЯвжЕ.
ГЩНЧЕФе§ЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪпЙћОЯњЩЬЯњЪлФГжжЪпЙћЃЌЪлМлЮЊУПЙЋНя25дЊЃЌГЩБОЮЊУПЙЋНя15дЊ.ЯњЪлзкжМЪЧЕБЬьНјЛѕЕБЬьЯњЪл.ШчЙћЕБЬьТєВЛГіШЅЃЌЮДЪлГіЕФШЋВПНЕМлвдУПЙЋНя10дЊДІРэЭъ.ИљОнвдЭљЕФЯњЪлЧщПіЃЌЕУЕНШчЭМЫљЪОЕФЦЕТЪЗжВМжБЗНЭМЃК

ЃЈ1ЃЉИљОнЦЕТЪЗжВМжБЗНЭММЦЫуИУжжЪпЙћШеашЧѓСПЕФЦНОљЪ§![]() ЃЈЭЌвЛзщжаЕФЪ§ОнгУИУзщЧјМфжаЕужЕДњБэЃЉЃЛ
ЃЈЭЌвЛзщжаЕФЪ§ОнгУИУзщЧјМфжаЕужЕДњБэЃЉЃЛ
ЃЈ2ЃЉИУОЯњЩЬФГЬьЙКНјСЫ250ЙЋНяетжжЪпЙћЃЌМйЩшЕБЬьЕФашЧѓСПЮЊ![]() ЙЋНя
ЙЋНя![]() ЃЌРћШѓЮЊ
ЃЌРћШѓЮЊ![]() дЊ.Чѓ
дЊ.Чѓ![]() Йигк
Йигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂНсКЯЦЕТЪЗжВМжБЗНЭМЙРМЦРћШѓ
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂНсКЯЦЕТЪЗжВМжБЗНЭМЙРМЦРћШѓ![]() ВЛаЁгк1750дЊЕФИХТЪ.
ВЛаЁгк1750дЊЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБШ§РтжљABCЉA1B1C1жаЃЌACЃНBCЃНAA1ЃН3ЃЌACЁЭBCЃЌЕуMдкЯпЖЮABЩЯЃЎ
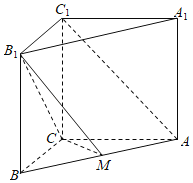
ЃЈ1ЃЉШєMЪЧABжаЕуЃЌжЄУїAC1ЁЮЦНУцB1CMЃЛ
ЃЈ2ЃЉЕБBM![]() ЪБЃЌЧѓжБЯпC1A1гыЦНУцB1MCЫљГЩНЧЕФе§ЯвжЕЃЎ
ЪБЃЌЧѓжБЯпC1A1гыЦНУцB1MCЫљГЩНЧЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЮоЧюЪ§Са![]() жаЃЌ
жаЃЌ![]() ЪЧИјЖЈЕФе§ећЪ§ЃЌ
ЪЧИјЖЈЕФе§ећЪ§ЃЌ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈЂёЃЉШє![]() ЃЌаДГі
ЃЌаДГі![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈЂђЃЉжЄУїЃКЪ§Са![]() жаДцдкжЕЮЊ
жаДцдкжЕЮЊ![]() ЕФЯюЃЛ
ЕФЯюЃЛ
ЃЈЂѓЃЉжЄУїЃКШє![]() ЛЅжЪЃЌдђЪ§Са
ЛЅжЪЃЌдђЪ§Са![]() жаБигаЮоЧюЖрЯюЮЊ
жаБигаЮоЧюЖрЯюЮЊ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХЁАББОЉАЫЗжжгЁБдкКЋЙњЦНВ§ЖЌАТЛсОЊбоССЯрЃЌЖЌАТЛсе§ЪННјШыСЫББОЉжмЦкЃЌШЋЩчЛсЖдЖЌАТЛсЕФШШЧщПеЧАИпеЧ.
ЃЈ1ЃЉЮЊгНгЖЌАТЛсЃЌФГЩчЧјЛ§МЋЭЦЖЏЖЌАТЛсЯюФПдкЩчЧјЧрЩйФъжаЕФЦеМАЃЌВЂЭГМЦСЫНќЮхФъРДБОЩчЧјЖЌАТЯюФПЧрЩйФъАЎКУепЕФШЫЪ§![]() ЃЈЕЅЮЛЃКШЫЃЉгыЪБМф
ЃЈЕЅЮЛЃКШЫЃЉгыЪБМф![]() ЃЈЕЅЮЛЃКФъЃЉЃЌСаБэШчЯТЃК
ЃЈЕЅЮЛЃКФъЃЉЃЌСаБэШчЯТЃК

вРОнБэИёИјГіЕФЪ§ОнЃЌЪЧЗёПЩгУЯпадЛиЙщФЃаЭФтКЯ![]() гы
гы![]() ЕФЙиЯЕЃЌЧыМЦЫуЯрЙиЯЕЪ§
ЕФЙиЯЕЃЌЧыМЦЫуЯрЙиЯЕЪ§![]() ВЂМгвдЫЕУї(МЦЫуНсЙћОЋШЗЕН0.01).
ВЂМгвдЫЕУї(МЦЫуНсЙћОЋШЗЕН0.01).
(Шє![]() ЃЌдђЯпадЯрЙиГЬЖШКмИпЃЌПЩгУЯпадЛиЙщФЃаЭФтКЯЃЉ
ЃЌдђЯпадЯрЙиГЬЖШКмИпЃЌПЩгУЯпадЛиЙщФЃаЭФтКЯЃЉ
ИНЃКЯрЙиЯЕЪ§ЙЋЪН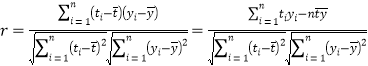 ЃЌВЮПМЪ§Он
ЃЌВЮПМЪ§Он![]() .
.
ЃЈ2ЃЉФГБљбЉдЫЖЏгУЦЗзЈгЊЕъЮЊЮќв§ЙуДѓБљбЉАЎКУепЃЌЬиЭЦГіСНжжДйЯњЗНАИ.
ЗНАИвЛ:УПТњ600дЊПЩМѕ100дЊЃЛ
ЗНАИЖў:Н№ЖюГЌЙ§600дЊПЩГщНБШ§ДЮЃЌУПДЮжаНБЕФИХТЪЭЌЮЊ![]() ЃЌЧвУПДЮГщНБЛЅВЛгАЯьЃЌжаНБ1ДЮДђ9елЃЌжаНБ2ДЮДђ8елЃЌжаНБ3ДЮДђ7ел. v
ЃЌЧвУПДЮГщНБЛЅВЛгАЯьЃЌжаНБ1ДЮДђ9елЃЌжаНБ2ДЮДђ8елЃЌжаНБ3ДЮДђ7ел. v
СНЮЛЙЫПЭЖМЙКТђСЫ1050дЊЕФВњЦЗЃЌВЂЧвЖМбЁдёЕкЖўжжгХЛнЗНАИЃЌЧѓжСЩйгавЛУћЙЫПЭБШбЁдёЗНАИвЛИќгХЛнЕФИХТЪЃЛ
ЂкШчЙћФуДђЫуЙКТђ1000дЊЕФБљбЉдЫЖЏгУЦЗЃЌЧыДгЪЕМЪИЖПюН№ЖюЕФЪ§бЇЦкЭћЕФНЧЖШЗжЮігІИУбЁдёФФжжгХЛнЗНАИ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§РтзЖ![]() жаЃЌвбжЊ
жаЃЌвбжЊ![]() ЪЧе§Ш§НЧаЮЃЌЦНУц
ЪЧе§Ш§НЧаЮЃЌЦНУц![]() ЦНУц
ЦНУц![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() дкРт
дкРт![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() .
.
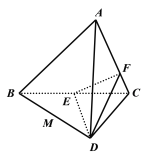
ЃЈ1ЃЉЧѓжЄЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЮЪ
ЕФжаЕуЃЌЮЪ![]() ЩЯЪЧЗёДцдквЛЕу
ЩЯЪЧЗёДцдквЛЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЦНУц
ЦНУц![]() ЃПШєДцдкЃЌЫЕУїЕу
ЃПШєДцдкЃЌЫЕУїЕу![]() ЕФЮЛжУЃЛШєВЛДцдкЃЌЪдЫЕУїРэгЩ.
ЕФЮЛжУЃЛШєВЛДцдкЃЌЪдЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЁАСшдЦБЁБРКЧђЖгЕФГЩдБРДздбЇаЃИпвЛЁЂИпЖўЙВ10ИіАрЕФ12ЮЛЭЌбЇЃЌЦфжаИпвЛЃЈ3ЃЉАрЁЂИпЖўЃЈ3ЃЉИїГі2ШЫЃЌЦфгрАрМЖИїГі1ШЫЃЌет12ШЫжавЊбЁ6ШЫЮЊжїСІЖгдБЃЌдђет6ШЫРДздВЛЭЌЕФАрМЖЕФИХТЪЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫМЭФюЁАвЛДјвЛТЗЁБГЋвщЬсГіЮхжмФъ,ФГГЧЪаОйАьСЫвЛГЁжЊЪЖОКШќ,ЮЊСЫСЫНтЪаУёЖдЁАвЛДјвЛТЗЁБжЊЪЖЕФеЦЮеЧщПі,ДгЛиЪеЕФгааЇД№ОэжаАДЧрФъзщКЭРЯФъзщИїЫцЛњГщШЁСЫ40ЗнД№Оэ,ЗЂЯжГЩМЈЖМдк![]() Фк,ЯжНЋГЩМЈАДЧјМф
Фк,ЯжНЋГЩМЈАДЧјМф![]() ,
,![]() ,
,![]() ,
,![]() ЃЌ
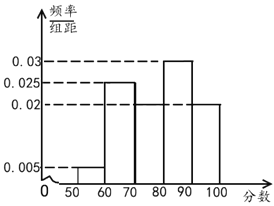
ЃЌ![]() НјааЗжзщ,ЛцжЦГЩШчЯТЕФЦЕТЪЗжВМжБЗНЭМЃЎ
НјааЗжзщ,ЛцжЦГЩШчЯТЕФЦЕТЪЗжВМжБЗНЭМЃЎ
ЧрФъзщ

жаРЯФъзщ
(1)РћгУжБЗНЭМЙРМЦЧрФъзщЕФжаЮЛЪ§КЭРЯФъзщЕФЦНОљЪ§ЃЛ
(2)ДгЧрФъзщ![]() ,
,![]() ЕФЗжЪ§ЖЮжа,АДЗжВуГщбљЕФЗНЗЈЫцЛњГщШЁ5ЗнД№Оэ,дйДгжабЁГі3ЗнД№ОэЖдгІЕФЪаУёВЮМгеўИЎзщжЏЕФзљЬИЛс,ЧѓбЁГіЕФ3ЮЛЪаУёжага2ЮЛРДзд
ЕФЗжЪ§ЖЮжа,АДЗжВуГщбљЕФЗНЗЈЫцЛњГщШЁ5ЗнД№Оэ,дйДгжабЁГі3ЗнД№ОэЖдгІЕФЪаУёВЮМгеўИЎзщжЏЕФзљЬИЛс,ЧѓбЁГіЕФ3ЮЛЪаУёжага2ЮЛРДзд![]() ЗжЪ§ЖЮЕФИХТЪЃЎ
ЗжЪ§ЖЮЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com