
分析 (1)求出f(x)的分段函数的形式,解不等式即可;
(2)问题转化为m≤2|x+1|-|2x-1|-x,令t(x)=2|x+1|-|2x-1|-x,求出t(x)的最小值,求出m的范围即可.
解答 解:(1)m=1时,f(x)=|x+1|+|2x-1|,
f(x)=$\left\{\begin{array}{l}{-3x,x<-1}\\{2-x,-1≤x≤\frac{1}{2}}\\{3x,x>\frac{1}{2}}\end{array}\right.$,
∴f(x)≥3,解得:x≤-1或x≥1;
(2)$\frac{1}{2}$f(x)≤|+1|⇒$\frac{1}{2}$|x+m|+$\frac{1}{2}$|2x-1|≤|x+1|,
∵x∈[m,2m2]且m>0,
∴$\frac{1}{2}$x+$\frac{m}{2}$≤|x+1|-$\frac{1}{2}$|2x-1|⇒m≤2|x+1|-|2x-1|-x,
令t(x)=2|x+1|-|2x-1|-x=$\left\{\begin{array}{l}{3x+1,0<x≤\frac{1}{2}}\\{3-x,x≥\frac{1}{2}}\end{array}\right.$,
由题意得$\left\{\begin{array}{l}{m>0}\\{m<{2m}^{2}}\end{array}\right.$⇒m>$\frac{1}{2}$,
t(x)min=t(2m2)≥m⇒m≤1,
∴$\frac{1}{2}$<m≤1.
点评 本题考查了函数恒成立问题,考查绝对值不等式问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{1}{2}$i | C. | $±\frac{1}{2}$ | D. | $±\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
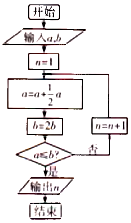 《算学启蒙》值中国元代数学家朱世杰撰写的一部数学启蒙读物,包括面积、体积、比例、开方、高次方程等问题,《算学启蒙》中有关于“松竹并生”的问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”,如图是源于其思想的一个程序框图,若输入a,b分别为8,2,则输出的n等于( )
《算学启蒙》值中国元代数学家朱世杰撰写的一部数学启蒙读物,包括面积、体积、比例、开方、高次方程等问题,《算学启蒙》中有关于“松竹并生”的问题:“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等”,如图是源于其思想的一个程序框图,若输入a,b分别为8,2,则输出的n等于( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 5 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
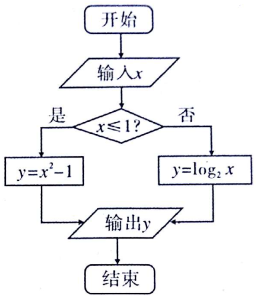 已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )
已知如图所示的程序框图的输入值x∈[-1,4],则输出y值的取值范围是( )| A. | [0,2] | B. | [-1,2] | C. | [-1,15] | D. | [2,15] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com