
(本小题满分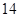 分)已知函数
分)已知函数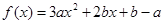 (
( ,
,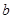 是不同时为零的常数).
是不同时为零的常数).
(1)当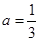 时,若不等式
时,若不等式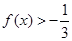 对任意
对任意 恒成立,求实数
恒成立,求实数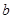 的取值范围;
的取值范围;
(2)求证:函数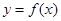 在
在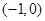 内至少存在一个零点.
内至少存在一个零点.
(1)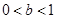 (2)
(2) 时易证结论;
时易证结论;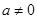 时,利用函数的零点存在定理可以证明结论成立.
时,利用函数的零点存在定理可以证明结论成立.
解析试题分析:(1)当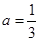 时,
时,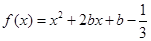 ,
,
由不等式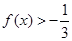 即
即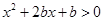 对任意
对任意 恒成立,
恒成立,
得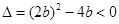 ,解得
,解得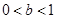 . ……5分
. ……5分
(2)证明:当 时,因为
时,因为 ,
,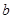 不同时为零,所以
不同时为零,所以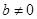 ,
,
所以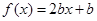 的零点为
的零点为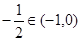 , ……6分
, ……6分
当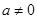 时,二次函数
时,二次函数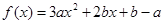 的对称轴方程为
的对称轴方程为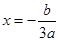 , ……7分
, ……7分
①若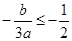 即
即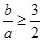 时,
时,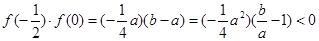 ,
,
∴函数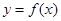 在
在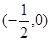 内至少存在一个零点. ……10分
内至少存在一个零点. ……10分
②若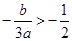 即
即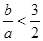 时,
时,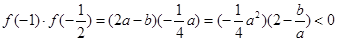 ,
,
∴函数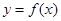 在
在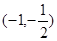 内至少存在一个零点. ……13分
内至少存在一个零点. ……13分
综上得:函数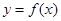 在
在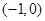 内至少存在一个零点. ……14分
内至少存在一个零点. ……14分
考点:本小题主要考查二次函数恒成立问题和函数零点存在定理的应用,考查学生的转化能力和运算求解能力以及分类讨论思想的应用.
点评:恒成立问题,一般转化为最值问题解决,而函数的零点存在定理能确定一定存在零点,但是确定不了存在几个零点.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)="2" sin (0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(1)求点A、B的坐标以及 ·
·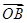 的值;
的值;
(2)没点A、B分别在角 、
、 的终边上,求tan(
的终边上,求tan(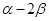 )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分14分) 本题共有2个小题,第1小题满分6分,第2小题满分8分.
已知函数 =
=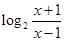 .
.
(1)判断函数 的奇偶性,并证明;
的奇偶性,并证明;
(2)求 的反函数
的反函数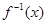 ,并求使得函数
,并求使得函数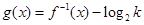 有零点的实数
有零点的实数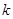 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知函数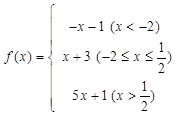 (
(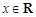 ),
),
(Ⅰ)求函数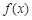 的最小值;
的最小值;
(Ⅱ)已知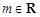 ,
,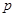 :关于
:关于 的不等式
的不等式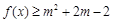 对任意
对任意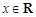 恒成立;
恒成立;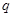 :函数
:函数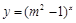 是增函数.若“
是增函数.若“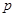 或
或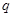 ”为真,“
”为真,“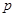 且
且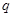 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题共12分)水库的蓄水量随时间而变化,现用t表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于t的近似函数关系式为
V(t)=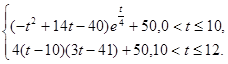
(Ⅰ)该水库的蓄水量小于50的时期称为枯水期.以i-1<t<i表示第i月份(i=1,2,…,12),问一年内哪几个月份是枯水期?
(Ⅱ)求一年内该水库的最大蓄水量(取e=2.7计算).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com