练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    函数f(x)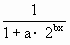＝的定义域为R，且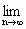f(－n)＝0(n∈N)．

    (1)求证：a＞0，b＜0；

    (2)(文)若f(1)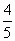＝且f(0)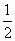＝，求证：f(1)＋f(2)＋…＋f(n)＞n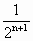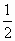＋－(n∈N)．

    (理)若f(1)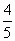＝，且f(x)在［0，1]上的最小值为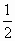，求证：f(1)＋f(2)＋…＋f(n)＞n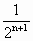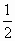＋－(n∈N)．

    答案：
    解析：

    		 　　(1)∵f(x)定义域为R，∴1＋a2bx≠0，即a≠－2－bx而x∈R，∴a≥0

    　　(1)∵f(x)定义域为R，∴1＋a2bx≠0，即a≠－2－bx而x∈R，∴a≥0．

    　　若a＝0，则f(x)＝1与f(－n)＝0矛盾，∴a＞0，

    　　∴f(－n)＝＝

    　　∴2－b＞1即b＜0，故a＞0，b＜0．

    　　(2)(文)∵f(0)＝，即＝，∴a＝1，f(1)＝＝，∴2b＝，

    　　∴b＝－2．∴f(x)＝＝＝1－．

    　　当k∈N时，f(k)＝1－＞1－　　∴f(1)＋f(2)＋f(3)＋…＋f(n)＞n－(＋＋)＝n＋－．

    　　(理)由(1)知f(x)在[0，1]上为增函数，∴f(0)＝，即＝，∴a＝1，

    　　f(1)＝＝，　　∴2b＝，∴b＝－2．

    　　∴f(x)＝＝＝1－．

    　　当k∈N时，f(k)＝1－＞1－．∴f(1)＋f(2)＋f(3)＋…＋f(n)＞n－(＋＋)＝n＋－．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    设f(x)＝是R上的奇函数．

    (1)求a的值；

    (2)求f(x)的反函数f－1(x)；

    (3)对任意给的k∈R+，解不等式f－1(x)＞log2．

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    函数f(x)＝－sin2x＋sinx＋a，若1≤f(x)≤，对一切x∈R恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：2004年高考教材全程总复习试卷·数学 题型：044

    函数f(x)的定义域为D，如果存在x0∈D，使f(x0)＝x0，则称点(x0，x0)为函数f(x)图象上的不动点．

    (1)试证明：若定义在R上的奇函数f(x)的图象上存在有限个不动点，则不动点有奇数个．

    (2)若函数f(x)＝的图象上有两个关于直线x＋y＝3对称的不动点，求a的值．

    查看答案和解析>>

    科目：高中数学 来源：安徽省蚌埠二中2007届第二次月考试卷、数学(文) 题型：044

    解答题：

    f(x)是定义在(0，＋)上的增函数，且对任意正实数x，y都有f(xy)＝f(x)＋f(y)，解关于x的不等式f(logx)0＜0

    查看答案和解析>>

    同步练习册答案