
分析 (1)根据抛物线的性质求出p的值,求出抛物线的解析式,从而求出P,F的坐标即可;
(2)①联立方程组得到y1+y2=-10,y1y2=-10b,计算$\overrightarrow{PA}•\overrightarrow{PB}$的表达式,从而求出b的值,求出直线AB的方程即可;
②设出A、B的坐标,根据kPA•kBP=-1,得到关于AB的方程,即y-y1=$\frac{{y}_{2}-{y}_{1}}{\frac{{y}_{1}^{2}}{4}•\frac{{y}_{2}^{2}}{4}}$(x1-x2),整理即可.
解答 解:(1)∵y2=2px(p>0)上一点P(1,t)(t>0)到焦点F的距离等于2,
∴|FP|=1+$\frac{p}{2}$=2,解得p=2,
∴y2=4x,
∴P(1,2),F(1,0),
(2)①令lAB:y=-$\frac{2}{5}x$+b,
∴$\left\{\begin{array}{l}{y=-\frac{2}{5}x+b}\\{{y}^{2}=4x}\end{array}\right.$,∴y=-$\frac{3}{5}$•$\frac{{y}^{2}}{4}$+b,
∴20y=-2y2+20b,
∴y2+10y-10b=0,
∴y1+y2=-10,y1y2=-10b,
又∵PA⊥PB,
∴$\overrightarrow{PA}•\overrightarrow{PB}$=(x1-1,y1-2)•(x2-1,y2-2)
=(x1-1)(x2-1)+(y1-2)(y2-2)
=$\frac{1}{16}$${y}_{1}^{2}•{y}_{2}^{2}$-$\frac{1}{4}$(${y}_{1}^{2}$+${y}_{2}^{2}$)+1+y1y2-2(y1+y2)+4=0,
∴$\frac{100}{16}$b2-$\frac{1}{4}$(100+20b)+1-10b+24=0,
解得b=$\frac{12}{5}$或b=0,
∴直线lAB:y=-$\frac{2}{5}$x+$\frac{12}{5}$(过点P,舍去),或y=-$\frac{2}{5}$x,
∴直线AB的方程;y=-$\frac{2}{5}$x,
②A($\frac{1}{4}{y}_{1}^{2}$,y1),B($\frac{1}{4}$${y}_{2}^{2}$,y2),
∵kPA•kBP=-1,
∴$\frac{{y}_{1}-2}{\frac{{y}_{1}^{2}}{4}-1}•\frac{{y}_{2}-2}{\frac{{y}_{2}^{2}}{4}-1}$=-1,
∴$\frac{4}{2+{y}_{1}}•\frac{4}{2+{y}_{2}}$=-1,
∴16=-(y1y2+2y1+2y2+4),
∴y1y2=-20-2(y1+y2),
∵lAB:y-y1=$\frac{{y}_{2}-{y}_{1}}{\frac{{y}_{1}^{2}}{4}•\frac{{y}_{2}^{2}}{4}}$(x1-x2),
∴y=y1+$\frac{4x}{{y}_{1}{+y}_{2}}$-$\frac{{{y}_{1}}^{2}}{{{y}_{1}+y}_{2}}$=$\frac{4x}{{y}_{1}{+y}_{2}}$-$\frac{{{y}_{1}y}_{2}}{{y}_{1}{+y}_{2}}$=$\frac{1}{{y}_{1}{+y}_{2}}$[4x-20-2(y1+y2)],
∴x=5时,y=-2,即过定点(5,-2).
点评 本题考查了抛物线的性质,考查直线和抛物线的关系,直线的垂直以及转化思想,是一道综合题.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
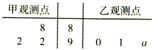 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com