Question

6．已知抛物线E：y²=4x的焦点为F，点C（-1，0），过点F的直线l与抛物线E相交于A，B两点，若AB⊥BC，则|AF|-|BF|=（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 由AB⊥BC，利用向量垂直与数量积间的关系列式求得B的横坐标，将直线AB的方程代入抛物线方程，利用韦达定理求得A的横坐标，分别表示出|AF|，|BF|，则|AF|-|BF|可求．

解答 解：如图，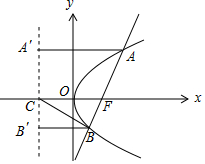

设A（x₁，y₁），B（x₂，y₂），
由AB⊥BC，得$\overrightarrow{BC}•\overrightarrow{BF}=（-1-{x}_{2}，-{y}_{2}）•（1-{x}_{2}，-{y}_{2}）=0$，
即${{x}_{2}}^{2}-1+{{y}_{2}}^{2}=0$，
由y₂²=4x₂，则x₂²+4x₂-1=0，由x₂＞0，得x₂=-2+$\sqrt{5}$，
由AB与x轴不垂直，设直线AB的方程y=k（x-1），
联立$\left\{\begin{array}{l}{y=k（x-1）}\\{{y}^{2}=4x}\end{array}\right.$，整理得：k²x²-（2k²+4）x+k²=0，
则x₁x₂=1，得x₁=$\frac{1}{{x}_{2}}=\frac{1}{-2+\sqrt{5}}$=2+$\sqrt{5}$，
∴|AF|-|BF|=（x₁+1）-（x₂+1）=（2+$\sqrt{5}$+1）-（-2+$\sqrt{5}$+1）=4，
故选：D．

点评 本题考查抛物线简单几何性质，考查抛物线的焦点弦公式，直线与抛物线的位置关系的应用，考查计算能力，属于中档题．