
已知椭圆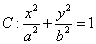
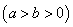 的右焦点
的右焦点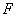
 ,长轴的左、右端点分别为
,长轴的左、右端点分别为 ,且
,且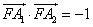 .
.
(Ⅰ)求椭圆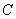 的方程;
的方程;
(Ⅱ)过焦点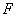 斜率为
斜率为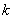
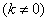 的直线
的直线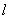 交椭圆
交椭圆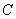 于
于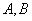 两点,弦
两点,弦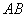 的垂直平分线与
的垂直平分线与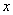 轴相交于点
轴相交于点 . 试问椭圆
. 试问椭圆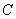 上是否存在点
上是否存在点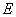 使得四边形
使得四边形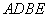 为菱形?若存在,试求点
为菱形?若存在,试求点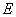 到
到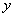 轴的距离;若不存在,请说明理由.
轴的距离;若不存在,请说明理由.
科目:高中数学 来源: 题型:
设集合A={-1, 0, 1},集合B={0, 1, 2, 3},定 义A*B={(x, y)| x∈A∩B, y∈A∪B},则A*B中元素个数是( )
义A*B={(x, y)| x∈A∩B, y∈A∪B},则A*B中元素个数是( )
A.7 B.10 C.25 D.52
查看答案和解析>>
科目:高中数学 来源: 题型:
数列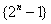 的前
的前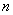 项
项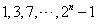 组成集合
组成集合 ,从集合
,从集合 中任取
中任取
 个数,其所有可能的
个数,其所有可能的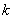 个数的乘积的和为
个数的乘积的和为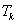 (若只取一个数,规定乘积为此数本身),记
(若只取一个数,规定乘积为此数本身),记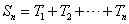 .例如当
.例如当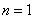 时,
时,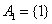 ,
,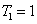 ,
,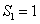 ;当
;当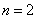 时,
时,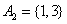 ,
,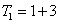 ,
,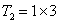 ,
, .则当
.则当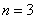 时,
时,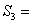 ;试写出
;试写出 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
 分享到
分享到百度分享
4.执行如图所示的程序框图,输出的S值为( )
(A)
(B)

(C)
(D)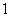
|
查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |