练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)=3ax2+2bx+c,a+b+c=0,且f(0)·f(1)>0.
    (1)求证:-2<<-1.
    (2)若x1,x2是方程f(x)=0的两个实根,求|x1-x2|的取值范围.

    (1)见解析  (2) [,)

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    我国辽东半岛普兰附近的泥炭层中，发掘出的古莲子，至今大部分还能发芽开花，这些古莲子是多少年以前的遗物呢？要测定古物的年代，可用放射性碳法．在动植物的体内都含有微量的放射性14C，动植物死亡后，停止了新陈代谢，14C不再产生，且原有的14C会自动衰变，经过5570年(叫做14C的半衰期)，它的残余量只有原始量的一半，经过科学家测定知道，若14C的原始含量为a，则经过t年后的残余量a′(与a之间满足a′＝a·e－kt)．现测得出土的古莲子中14C残余量占原量的87.9%，试推算古莲子的生活年代．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某商场销售某种商品的经验表明，该商品每日的销售量y(单
    位：千克)与销售价格x(单位：元/千克)满足关系式y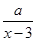＝＋10(x－6)2，其中3<x<6，a为常数．已知销售价格为5元/千克时，每日可售出该商品11千克．
    ①求a的值；
    ②若该商品的成本为3元/千克，试确定销售价格x的值，使商场每日销售该商品所获得的利润最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=x2+10x(万元).当年产量不小于80千件时,C(x)=51x+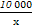-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
    (1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式.
    (2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    东海水晶制品厂去年的年产量为10万件,每件水晶产品的销售价格为100元,固定成本为80元.从今年起,工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本.预计产量每年递增1万件,每件水晶产品的固定成本g(n)与科技成本的投入次数n的关系是g(n)=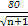.若水晶产品的销售价格不变,第n次投入后的年利润为f(n)万元.
    (1)求出f(n)的表达式.
    (2)求从今年算起第几年利润最高?最高利润为多少万元?

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知二次函数f(x)=x2+(2a-1)x+1-2a.
    (1)判断命题“对于任意的a∈R(R为实数集),方程f(x)=1必有实数根”的真假,并写出判断过程.
    (2)若y=f(x)在区间(-1,0)及(0,)内各有一个零点,求实数a的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝－x2＋2ex＋m－1，g(x)＝x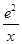＋ (x>0)．
    (1)若g(x)＝m有零点，求m的取值范围；
    (2)确定m的取值范围，使得g(x)－f(x)＝0有两个相异实根．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝x2＋bx＋c(b，c∈R)，对任意的x∈R，恒有f′(x)≤f(x)．
    (1)证明：当x≥0时，f(x)≤(x＋c)2；
    (2)若对满足题设条件的任意b，c，不等式f(c)－f(b)≤M(c2－b2)恒成立，求M的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某跨国饮料公司对全世界所有人均GDP（即人均纯收入）在0.5—8千美元的地区销售，该公司M饮料的销售情况的调查中发现：人均GDP处在中等的地区对该饮料的销售量最多，然后向两边递减.
    (1)下列几个模拟函数中（x表示人均GDP,单位：千美元；y表示年人均M饮料的销量，单位：升），用哪个来描述人均,饮料销量与地区的人均GDP的关系更合适？说明理由.

    A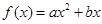． B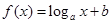． C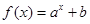． D．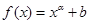
    (2)若人均GDP为1千美元时，年人均M饮料的销量为2升；人均GDP为4千美元时，年人均M饮料的销量为5升；把你所选的模拟函数求出来.;
    (3)因为M饮料在N国被检测出杀虫剂的含量超标，受此事件影响，M饮料在人均GDP不高于3千美元的地区销量下降5%，不低于6千美元的地区销量下降5%，其他地区的销量下降10%，根据（2）所求出的模拟函数，求在各个地区中，年人均M饮料的销量最多为多少？

    查看答案和解析>>

    同步练习册答案