已知函数f(x)＝－x2＋2ex＋m－1，g(x)＝x＋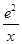
(x>0)．
(1)若g(x)＝m有零点，求m的取值范围；
(2)确定m的取值范围，使得g(x)－f(x)＝0有两个相异实根．
科目：高中数学 来源： 题型：解答题
对于函数f(x)，若存在x0∈R，使f(x0)＝x0成立，则称x0为f(x)的不动点，已知函数f(x)＝ax2＋(b＋1)x＋b－1(a≠0)．
(1)当a＝1，b＝－2时，求f(x)的不动点；
(2)若对任意实数b，函数f(x)恒有两个相异的不动点，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数f(x)=3ax2+2bx+c,a+b+c=0,且f(0)·f(1)>0.
(1)求证:-2<
<-1.
(2)若x1,x2是方程f(x)=0的两个实根,求|x1-x2|的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
(13分)某工厂某种产品的年固定成本为250万元，每生产x千件，需另投入成本C(x)，当年产量不足80千件时，C(x)＝
x2＋10x(万元)；当年产量不小于80千件时，C(x)＝51x＋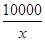
－1 450(万元)．每件商品售价为0.05万元．通过市场分析，该厂生产的商品能全部售完．
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式；
(2)年产量为多少千件时，该厂在这一商品的生产中所获利润最大？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，在C城周边已有两条公路l1，l2在点O处交汇．已知OC＝(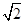
＋
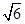)km，∠AOB＝75°，∠AOC＝45°，现规划在公路l1，l2上分别选择A，B两处为交汇点(异于点O)直接修建一条公路通过C城．设OA＝x km，OB＝y km.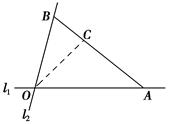
(1)求y关于x的函数关系式并指出它的定义域；
(2)试确定点A，B的位置，使△OAB的面积最小．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
对于定义域为A的函数f(x)，如果任意的x1，x2∈A，当x1＜x2时，都有f(x1)＜f(x2)，则称函数f(x)是A上的严格增函数；函数f(k)是定义在N*上，函数值也在N*中的严格增函数，并且满足条件f(f(k))＝3k.
(1)证明：f(3k)＝3f(k)；
(2)求f(3k－1)(k∈N*)的值；
(3)是否存在p个连续的自然数，使得它们的函数值依次也是连续的自然数；若存在，找出所有的p值，若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
设函数f(x)＝ax2＋bx＋b－1(a≠0)．
(1)当a＝1，b＝－2时，求函数f(x)的零点；
(2)若对任意b∈R，函数f(x)恒有两个不同零点，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知
是正数，
，
，
．
（Ⅰ）若成等差数列，比较
与
的大小；
（Ⅱ）若
，则三个数中，哪个数最大，请说明理由；
（Ⅲ）若
，
，
（
），且
，
，
的整数部分分别是
求所有
的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
．
时，判断
在
的单调性，并用定义证明．
，不等式
恒成立，求
的取值范围；