练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在C城周边已有两条公路l1，l2在点O处交汇．已知OC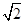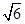＝(＋)km，∠AOB＝75°，∠AOC＝45°，现规划在公路l1，l2上分别选择A，B两处为交汇点(异于点O)直接修建一条公路通过C城．设OA＝x km，OB＝y km.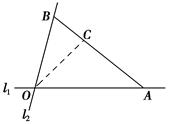

    (1)求y关于x的函数关系式并指出它的定义域；
    (2)试确定点A，B的位置，使△OAB的面积最小．

    （1）y＝(x＞2)（2）4(＋1) km2.

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    化简下列各式(其中各字母均为正数)：
    (1)1.5－×0＋80.25×＋(×)6－；
    (2)；
    (3)

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=x2+10x(万元).当年产量不小于80千件时,C(x)=51x+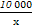-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
    (1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式.
    (2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知二次函数f(x)=x2+(2a-1)x+1-2a.
    (1)判断命题“对于任意的a∈R(R为实数集),方程f(x)=1必有实数根”的真假,并写出判断过程.
    (2)若y=f(x)在区间(-1,0)及(0,)内各有一个零点,求实数a的范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝－x2＋2ex＋m－1，g(x)＝x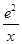＋ (x>0)．
    (1)若g(x)＝m有零点，求m的取值范围；
    (2)确定m的取值范围，使得g(x)－f(x)＝0有两个相异实根．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某兴趣小组要测量电视塔AE的高度H(单位：m)．如示意图，垂直放置的标杆BC的高度h＝4 m，仰角∠ABE＝α，∠ADE＝β.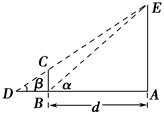
     
    (1)该小组已测得一组α，β的值，算出了tan α＝1.24，tan β＝1.20，请据此算出H的值；
    (2)该小组分析若干测得的数据后，认为适当调整标杆到电视塔的距离d(单位：m)，使α与β之差较大，可以提高测量精度．若电视塔的实际高度为125 m，试问d为多少时，α－β最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝x2＋bx＋c(b，c∈R)，对任意的x∈R，恒有f′(x)≤f(x)．
    (1)证明：当x≥0时，f(x)≤(x＋c)2；
    (2)若对满足题设条件的任意b，c，不等式f(c)－f(b)≤M(c2－b2)恒成立，求M的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度)．设该蓄水池的底面半径为r米，高为h米，体积为V立方米．假设建造成本仅与表面积有关，侧面积的建造成本为100元/平方米，底面的建造成本为160元/平方米，该蓄水池的总建造成本为12 000π元(π为圆周率)．
    (1)将V表示成r的函数V(r)，并求该函数的定义域；
    (2)讨论函数V(r)的单调性，并确定r和h为何值时该蓄水池的体积最大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数的定义域为集合.
    （1）若函数的定义域也为集合，的值域为，求；
    （2）已知,若,求实数的取值范围.

    查看答案和解析>>

    同步练习册答案