
| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |
分析 先判断命题p,q的真假,再由复合命题真假判断的真值表,可得答案.
解答 解:函数f(x)=${(\frac{1}{2})}^{x}$为减函数,
若x>y,则${(\frac{1}{2})^x}<{(\frac{1}{2})^y}$,
故命题p:为真命题;
m>1时,x2+mx+1=0不一定有两个根,
则命题q:函数 y=x2+mx+1有两个零点为假命题.
则:(1)p∧q为假命题;
(2)p∨q为真命题;
(3)p∧(¬q)为真命题;
(4)(¬p)∨q为假命题,
故选:C.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,指数函数的图象和性质,方程根的存在性与个数判断等知识点,难度中档.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $2\sqrt{3}$ | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -1 | C. | -$\frac{3}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
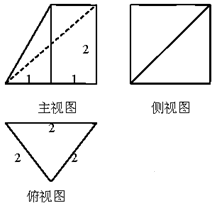
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
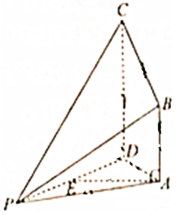 如图,在四棱锥P-ABCD中,AD=AP,CD=2AB,CD⊥平面APD,AB∥CD,E为PD的中点.
如图,在四棱锥P-ABCD中,AD=AP,CD=2AB,CD⊥平面APD,AB∥CD,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 0 | C. | $\frac{13}{6}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com