
分析 (Ⅰ)通过讨论x的范围,求出各个区间上的不等式的解集,取并集即可;
(Ⅱ)法一:求出f(x)的分段函数的形式,令y=x-a,通过讨论求出a的范围即可;
法二:设g(x)=f(x)-x,问题转化为-a≥g(x)max,求出g(x)的最大值,得到a的范围即可.
解答 解:(Ⅰ)f(x)=|x+2|-2|x-1|≥-2,
当x≤-2时,x-4≥-2,即x≥2,所以x∈∅;
当-2<x<1时,3x≥-2,即x≥-$\frac{2}{3}$,所以-$\frac{2}{3}$≤x<1;
当x≥1时,-x+4≥-2,即x≤6,所以1≤x≤6;
综上,不等式f(x)≥-2的解集为M={x|-$\frac{2}{3}$≤x≤6};
(Ⅱ)f(x)=$\left\{\begin{array}{l}{x-4,x≤-2}\\{3x,-2<x<1}\\{-x+4,x≥1}\end{array}\right.$,
令y=x-a,当直线经过点(1,3)时,-a=2,
所以当-a≥2,即a≤-2时成立;
当-a<2即a>-2时,令-x+4=x-a,得x=2+$\frac{a}{2}$,
所以a≥2+$\frac{a}{2}$,即a≥4,
综上,a≤-2或a≥4.
解法二:(Ⅰ)同解法一,
(Ⅱ)设g(x)=f(x)-x=$\left\{\begin{array}{l}{-2x+4,x≥1}\\{2x,-2<x<1}\\{-4,x≤-2}\end{array}\right.$,
因为对任意x∈[a,+∞),都有f(x)≤x-a成立,
所以-a≥g(x)max,
①当a>1时,g(x)max=g(a)=-2a+4,
所以-a≥-2a+4,所以a≥4,符合a>1.
②当a≤1时,g(x)max=g(1)=2,
所以-a≥2,所以a≤-2,符合a≤1,
综上,实数a的取值范围是(-∞,-2]∪[4,+∞).
点评 本小题考查绝对值不等式的解法与性质等基础知识,考查运算求解能力、推理论证能力,考查分类与整合思想、化归与转化思想等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
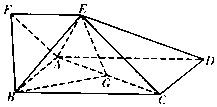 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,点G为AC的中点.
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,点G为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1)(3) | B. | (1)(4) | C. | (2)(3) | D. | (2)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com