
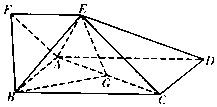
 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,点G为AC的中点.
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}$AD=2,点G为AC的中点.分析 (Ⅰ)推导出CD⊥AE,ED⊥AE,从而AE⊥平面DCE,由此能证明平面BAE⊥平面DCE.
(Ⅱ)作EN⊥AD,垂足为N,三棱锥B-AEG的体积为VB-AEG=VE-ABG,由此能求出结果.
解答 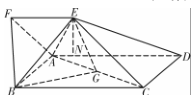 证明:(Ⅰ)∵四边形ABCD为矩形,且平面ABCD⊥平面AFED,
证明:(Ⅰ)∵四边形ABCD为矩形,且平面ABCD⊥平面AFED,
∴CD⊥平面AFED,∴CD⊥AE,
∵∠AED=90°,∴ED⊥AE,
又∵EO∩CD=D,∴AE⊥平面DCE,
又AE?平面BAE,∴平面BAE⊥平面DCE.…(6分)
解:(Ⅱ)作EN⊥AD,垂足为N,
由平面ABCD⊥平面AFED,平面ABCD∩平面AFED=AD.
得EN⊥平面ABCD,即EN为三棱锥E-ABG的高.
∵在△AEF中,AF=FE,∠AFE=60°,∴△AEF是正三角形,AE=2,
由EF∥AD,知∠EAD=60°,∴$EN=AE•sin60°=\sqrt{3}$,
∴三棱锥B-AEG的体积为:
${V_{B-AEG}}={V_{E-ABG}}=\frac{1}{3}{S_{△ABG}}•EN=\frac{1}{3}×\frac{1}{2}×2×2×\sqrt{3}=\frac{{2\sqrt{3}}}{3}$.…••(12分)
点评 本题考查面面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4032}{2017}$ | B. | $\frac{4028}{2015}$ | C. | $\frac{2015}{2016}$ | D. | $\frac{2014}{2015}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
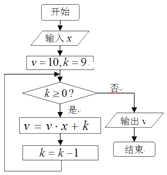 秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出的v值为( )
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入x的值为2,则输出的v值为( )| A. | 9×210-2 | B. | 9×210+2 | C. | 9×211+2 | D. | 9×211-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | (1,3) | C. | [2,3) | D. | (1,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $2\sqrt{3}$ | D. | $4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com