
分析 (1)运用递推关系式a1=3,an+1=1+2Sn,求解即可.
(2)an+1=1+2Sn,①,an=1+2Sn-1,②,相减即可求解n≥2时,an=7×3n-2,验证n=1即可的通项公式.
(3)运用定义得出Tn=$\frac{1}{3}$+$\frac{2}{7}$+$\frac{3}{7×3}$$+\frac{4}{7×{3}^{2}}$$+\frac{5}{7×{3}^{3}}$+…+$\frac{n-1}{7×{3}^{n-3}}$+$\frac{n}{7×{3}^{n-2}}$,利用错位相减得出Tn=$\frac{16}{21}$$+\frac{3}{28}$(1-$\frac{1}{{3}^{n-2}}$)-$\frac{3n}{14×{3}^{n-1}}$<$\frac{16}{21}$$+\frac{3}{28}$=$\frac{73}{84}$$<\frac{9}{4}$,放缩即可证明.
解答 解:数列{an}的前n项和为Sn,a1=3,an+1=1+2Sn
(1)a2=1+2×3=7,a3=1+2(3+7)=21,a4=1+2(3+7+21)=63,
(2)an+1=1+2Sn,①
an=1+2Sn-1,②,
①-②得出:an+1-an=2an(n≥2)
即an+1=3an,(n≥2),
根据等比数列的性质得出:当n=1时,a1=3,n=2时,a2=7,
n≥2时,an=7×3n-2,
∴an=$\left\{\begin{array}{l}{3,n=1}\\{7×{3}^{n-2},n≥2}\end{array}\right.$
(3)∵bn=$\frac{n}{{a}_{n}}$,数列{bn}的前n项和Tn,
∴Tn=$\frac{1}{3}$+$\frac{2}{7}$+$\frac{3}{7×3}$$+\frac{4}{7×{3}^{2}}$$+\frac{5}{7×{3}^{3}}$+…+$\frac{n-1}{7×{3}^{n-3}}$+$\frac{n}{7×{3}^{n-2}}$,
令Gn=$\frac{2}{7}$+$\frac{3}{7×3}$$+\frac{4}{7×{3}^{2}}$$+\frac{5}{7×{3}^{3}}$+…+$\frac{n-1}{7×{3}^{n-3}}$+$\frac{n}{7×{3}^{n-2}}$,③
$\frac{1}{3}$Gn=$\frac{2}{7×3}$$+\frac{3}{7×{3}^{2}}$$+\frac{4}{7×{3}^{3}}$+…+$\frac{n-1}{7×{3}^{n-2}}$$+\frac{n}{7×{3}^{n-1}}$④,
③-④得出:$\frac{2}{3}$Gn=$\frac{2}{7}$+($\frac{1}{7×3}$$+\frac{1}{7×{3}^{2}}$$+\frac{1}{7×{3}^{3}}$+…+$\frac{1}{7×{3}^{n-2}}$)-$\frac{n}{7×{3}^{n-1}}$
=$\frac{2}{7}$+$\frac{1}{14}$(1-$\frac{1}{{3}^{n-2}}$)$-\frac{n}{7×{3}^{n-1}}$,
Gn=$\frac{3}{7}$$+\frac{3}{28}$(1-$\frac{1}{{3}^{n-2}}$)-$\frac{3n}{14×{3}^{n-1}}$,
Tn=$\frac{16}{21}$$+\frac{3}{28}$(1-$\frac{1}{{3}^{n-2}}$)-$\frac{3n}{14×{3}^{n-1}}$<$\frac{16}{21}$$+\frac{3}{28}$=$\frac{73}{84}$$<\frac{9}{4}$,
故数列{bn}的前n项和Tn<$\frac{9}{4}$.
点评 本题综合考察了数列的递推关系式,性质,求解和的问题,放缩法证明不等式,考察了学生的计算化简能力,难度较大.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
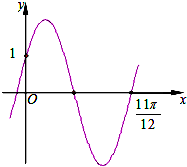
| A. | $f(x)=2sin({\frac{10}{11}x+\frac{π}{6}\;})$ | B. | $f(x)=2sin({\frac{10}{11}x-\frac{π}{6}\;})$ | ||
| C. | $f(x)=2sin({2x+\frac{π}{6}\;})$ | D. | $f(x)=2sin({2x-\frac{π}{6}\;})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com