练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．在△ABC中，如果sinA=$\sqrt{3}$sinC，B=30°，那么角A=120°．

    分析 由题意和正弦定理可得a=$\sqrt{3}$c，再由余弦定理可得b2=c2，代入cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$化简可得余弦值，可角A

    解答 解：∵sinA=$\sqrt{3}$sinC，
    ∴由正弦定理可得a=$\sqrt{3}$c，
    又∵B=30°，
    ∴由余弦定理可得b2=a2+c2-2accosB，
    代入数据可得b2=3c2+c2-3c2=c2，即b=c，
    ∴再由余弦定理可得cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$
    =$\frac{{c}^{2}+{c}^{2}-3{c}^{2}}{2{c}^{2}}$=-$\frac{1}{2}$，∴A=120°
    故答案为：120°．

    点评 本题考查解三角形，涉及正余弦定理的综合应用，属中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．在△ABC中，角A，B，C的对边分别为a，b，c，已知c=2，$C=\frac{π}{3}$．
    （1）若△ABC的面积为$\sqrt{3}$，求a，b；
    （2）若sinC+sin（B-A）=sin2A，求a，b．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．铁矿石A和B的含铁率a，冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表：
    ab（万吨）c（百万元）
    A50%13
    B70%0.56
    某冶炼厂至少要生产1.9（万吨）铁，若要求CO2的排放量不超过2（万吨），求购买铁矿石的最少费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知数列{an}的前n项和为Sn，a1=3，an+1=1+2Sn
    （1）a2，a3，a4的值；
    （2）求数列{an}的通项公式；
    （3）设bn=$\frac{n}{{a}_{n}}$，证明数列{bn}的前n项和Tn＜$\frac{9}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．设P为双曲线x2-$\frac{y^2}{12}$=1上的一点，F1、F2是该双曲线的两个焦点，若|PF1|：|PF2|=3：2，则△PF1F2的面积为12．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．在一组样本数据（x1，y1），（x2，y2），…（xn，yn）（n≥2，x1，x2，…，xn不全相等）的散点图中，若所有样本点（xi，yi）（i=1，2，…，n）都在直线y=2x+1上，则这组样本数据的样本相关系数为（　　）
    A．-1B．0C．2D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．使cosx=1-m有意义的m的取值范围为（　　）
    A．m≥0B．0≤m≤2C．-1＜m＜1D．m＜-1或m＞1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

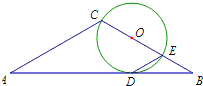    9．如图，在△ACB中，∠ACB=120°，AC=BC=3，点O在BC边上，且圆O与AB相切于点D，BC与圆O相交于点E，C，则∠EDB=30°，BE=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知复数z=（2m2-3m-2）+（m2-3m+2）i．当实数m取什么值时，复数z是：
    （1）0；   
    （2）虚数     
    （3）复平面内满足y=-x的点对应的复数．

    查看答案和解析>>

    同步练习册答案