
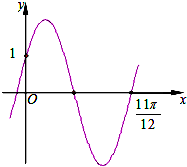
| A. | $f(x)=2sin({\frac{10}{11}x+\frac{π}{6}\;})$ | B. | $f(x)=2sin({\frac{10}{11}x-\frac{π}{6}\;})$ | ||
| C. | $f(x)=2sin({2x+\frac{π}{6}\;})$ | D. | $f(x)=2sin({2x-\frac{π}{6}\;})$ |
分析 由点(0,1)在函数图象上,可得1=2sinφ,结合|φ|<$\frac{π}{2}$,可得φ,又点($\frac{11π}{12}$,0)在函数图象上,可得0=2sin(ω$\frac{11π}{12}$+$\frac{π}{6}$),从而解得ω的一个值为2,从而得解.
解答 解:由函数图象可得:点(0,1)在函数图象上,故有:1=2sinφ,由于$,{|φ|<\frac{π}{2}}$,可得φ=$\frac{π}{6}$,
又点($\frac{11π}{12}$,0)在函数图象上,可得:0=2sin(ω$\frac{11π}{12}$+$\frac{π}{6}$),
由ω$\frac{11π}{12}$+$\frac{π}{6}$=2kπ,k∈Z,解得:ω=$\frac{24k-2}{11}$,k∈Z,ω>0,
当k=1时,可得:ω=2,
故选:C.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,确定ω的值是解题的关键,属于基本知识的考查.


科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{2},\sqrt{2}}$) | B. | (-$\sqrt{3},\sqrt{3}}$) | C. | (-∞,-$\sqrt{2}}$)∪(${\sqrt{2}$,+∞) | D. | (-∞,-$\sqrt{3}}$)∪(${\sqrt{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
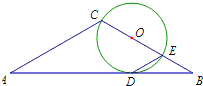 如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.
如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
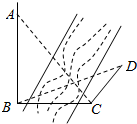 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)| A. | 10$\sqrt{2}$ | B. | 10$\sqrt{6}$ | C. | 10$\sqrt{3}$ | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com