
分析 根据定积分的几何意义,$\int_0^6{\sqrt{1-\frac{x^2}{36}}}$dx,表示以a=6,b=1焦点在x轴上的椭圆的面积的四分之一,再根据椭圆的面积公式S=πab,计算即可.
解答  解:$\int_0^6{\sqrt{1-\frac{x^2}{36}}}$dx,设1-$\frac{{x}^{2}}{36}$=y,y>0,$\frac{{x}^{2}}{36}$+y2=1,表示以a=6,b=1焦点在x轴上的椭圆的面积的四分之一,
解:$\int_0^6{\sqrt{1-\frac{x^2}{36}}}$dx,设1-$\frac{{x}^{2}}{36}$=y,y>0,$\frac{{x}^{2}}{36}$+y2=1,表示以a=6,b=1焦点在x轴上的椭圆的面积的四分之一,
如图所示,
∵S椭圆=πab=6π,
∴$\int_0^6{\sqrt{1-\frac{x^2}{36}}}$dx=$\frac{1}{4}$×6π=$\frac{3π}{2}$,
故答案为:$\frac{3π}{2}$.
点评 本题考查了定积分的几何意义,以及椭圆的面积公式,属于中档题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:选择题
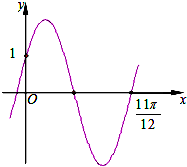
| A. | $f(x)=2sin({\frac{10}{11}x+\frac{π}{6}\;})$ | B. | $f(x)=2sin({\frac{10}{11}x-\frac{π}{6}\;})$ | ||
| C. | $f(x)=2sin({2x+\frac{π}{6}\;})$ | D. | $f(x)=2sin({2x-\frac{π}{6}\;})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | $({-∞,-\frac{1}{6}})$ | C. | $({-\frac{1}{6},+∞})$ | D. | (-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com