
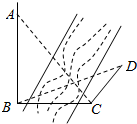
 如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)
如图,为测得河对岸塔AB的高,先在河岸上选一点C,使C在塔底B的正东方向上,测得点A的仰角为60°,再由点C沿北偏东15°方向走10m到位置D,测得∠BDC=45°,则塔AB的高是( )(单位:m)| A. | 10$\sqrt{2}$ | B. | 10$\sqrt{6}$ | C. | 10$\sqrt{3}$ | D. | 10 |
分析 设塔高为x米,根据题意可知在△ABC中,∠ABC=90°,∠ACB=60°,AB=x,从而有BC=$\frac{\sqrt{3}}{3}x$,在△BCD中,CD=10,∠BCD=105°,∠BDC=45°,∠CBD=30°,由正弦定理可求 BC,从而可求x即塔高.
解答 解:设塔高为x米,根据题意可知在△ABC中,∠ABC=90°,∠ACB=60°,AB=x,
从而有BC=$\frac{\sqrt{3}}{3}x$,AC=$\frac{2\sqrt{3}}{3}x$,
在△BCD中,CD=10,∠BCD=60°+30°+15°=105°,∠BDC=45°,∠CBD=30°
由正弦定理可得,$\frac{BC}{sin∠BDC}=\frac{CD}{sin∠CBD}$
可得,BC=$\frac{10sin45°}{sin30°}$=10$\sqrt{2}$=$\frac{\sqrt{3}}{3}x$
则x=10$\sqrt{6}$;
所以塔AB的高是10$\sqrt{6}$米;
故选:B.
点评 本题主要考查了正弦定理在实际问题中的应用,解决本题的关键是要把实际问题转化为数学问题,即正确建立数学模型,结合已知把题目中的数据转化为三角形中的数据,进而选择合适的公式进行求解.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:选择题
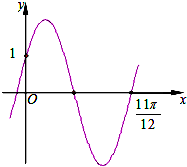
| A. | $f(x)=2sin({\frac{10}{11}x+\frac{π}{6}\;})$ | B. | $f(x)=2sin({\frac{10}{11}x-\frac{π}{6}\;})$ | ||
| C. | $f(x)=2sin({2x+\frac{π}{6}\;})$ | D. | $f(x)=2sin({2x-\frac{π}{6}\;})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
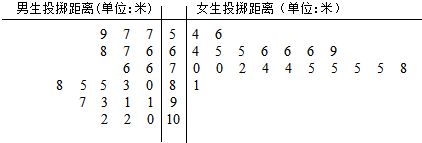
| 男生投掷距离(米) | … | [5.4,6.0) | [6.0,6.6) | [6.6,7.4) | [7.4,7.8) | [7.8,8.6) | [8.6,10.0) | [10.0,+∞) |
| 女生投掷距离(米) | … | [5.1,5.4) | [5.4,5.6) | [5.6,6.4) | [6.4,6.8) | [6.8,7.2) | [7.2,7.6) | [7.6,+∞) |
| 个人得分(分) | … | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30种 | B. | 35种 | C. | 42种 | D. | 48种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com