
某校中学生篮球队教练经常组织队员以三人为一组的运球上篮训练,要求每人接球后再传给别的队员,则运球中第一次传球的队员第五次接球刚好上篮的运球方式有 种.
10
【解析】设A,B,C为运球的三人,并且A队员为第一传球人, 那么A队员第五次接球刚好上篮的运球方式有三类,每类都分五步完成.
第一类:第一步,A队员向B,C队员进行第一次传球,有两种方式.
第二步,第三步,第四步,B,C队员之间进行第二,三,四次传球,各有一种方式.
第五步, B,C队员中一名队员第四次接球后传给A队员,有一各方式.根据乘法计数原理, 第一类共有2×1×1×1×1=2
第二类:第一步,A队员向B,C队员进行第一次传球,有两种方式
第二步,B或C队员接球后立即回传给A队员完成第二次传球,仅有一种方式
第三步,A队员向B,C队员进行第三次传球,有两种方式
第四步,B,C队员之间进行第四次传球,仅有一种方式.
第五步, B,C队员中一名队员第四次接球后传给A队员,仅有一种方式.根据乘法计数原理, 第二类共有2×1×2×1×1=4
第三类:第一步,A队员向B,C队员进行第一次传球,有两种方式
第二步,B,C队员之间进行第二次传球,仅有一种方式.
第三步,B或C队员接球后立即回传给A队员完成第三次传球,仅有一种方式
第四步,A队员向B,C队员进行第四次传球,有两种方式
根据乘法计数原理, 第三类共有2×1×1×2×1=4
根据加法计数原理, 运球方式有2+4+4=10种


科目:高中数学 来源:2015届上海市高二4月阶段测试数学试卷(解析版) 题型:解答题
定义:我们把椭圆的焦距与长轴的长度之比即 ,叫做椭圆的离心率.若两个椭圆的离心率
,叫做椭圆的离心率.若两个椭圆的离心率 相同,称这两个椭圆相似.
相同,称这两个椭圆相似.
(1)判断椭圆 与椭圆
与椭圆 是否相似?并说明理由;
是否相似?并说明理由;
(2)若椭圆
 与椭圆
与椭圆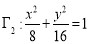 相似,求
相似,求 的值;
的值;
(3)设动直线 与(2)中的椭圆
与(2)中的椭圆 交于
交于 两点,试探究:在椭圆
两点,试探究:在椭圆 上是否存在异于
上是否存在异于 的定点
的定点 ,使得直线
,使得直线 的斜率之积为定值?若存在,求出定点
的斜率之积为定值?若存在,求出定点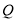 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科预测三(解析版) 题型:解答题
如图,PA,PB切⊙O于A,B两点,BC∥PA交⊙O于C,MC∥AB交⊙O于D,交PB,PA的延长线于M,Q.
(1)求证:AD∥PM
(2)设⊙O的半径长为1,PA=PB=2,求CD的长

查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科预测一(解析版) 题型:解答题
设函数f(x)=a·b,其中向量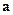
 ,向量
,向量
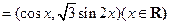 .
.
(1)求f(x)的最小正周期;
(2)在∆ABC中,a,b,c分别是角A,B,C的对边,f(A)=2,a=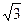 ,b+c=3,求b,c的长.
,b+c=3,求b,c的长.
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科预测一(解析版) 题型:选择题
设f(x)是奇函数,且在(0,+∞)内是增函数,又f(-3)=0,则(x-3)f(x-3)<0的解集是( )
A.(-3,0)或(3,+∞) B.(-3,3)
C.(0,3) D.(0,3)或(3,6)
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学理科算法和程序框图(解析版) 题型:选择题
执行如图所示的程序框图,如果输出S=3,那么判断框内应填入的条件是( )

A. k≤6
B. k≤7
C. k≤8
D. k≤9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com