
分析 (1)由三角函数恒等变换的应用化简函数解析式为$f(x)=sin(2x+\frac{2π}{3})$,利用正弦函数的单调性即可解得f(x)的递增区间.
(2)由$f(C)=sin(2C+\frac{2π}{3})=-\frac{{\sqrt{3}}}{2}$,解得$2C+\frac{2π}{3}=\frac{4π}{3}$或$\frac{5π}{3}$,可得C的值,由题意可得sinB-2sinA=0,由正弦定理得b=2a,分别由余弦定理,勾股定理即可解得a,b的值.
解答 解:(1)∵$f(x)=2cos(x+\frac{5π}{12})sin(x+\frac{π}{4})+\frac{1}{2}$
=2cos(x+$\frac{π}{2}$-$\frac{π}{3}$+$\frac{π}{4}$)sin(x+$\frac{π}{4}$)$+\frac{1}{2}$
=-2[sin(x+$\frac{π}{4}$)cos$\frac{π}{3}$-cos(x+$\frac{π}{4}$)sin$\frac{π}{3}$]sin(x+$\frac{π}{4}$)+$\frac{1}{2}$
=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x
=$sin(2x+\frac{2π}{3})$,
∴2k$π-\frac{π}{2}$≤2x$+\frac{2π}{3}$≤2k$π+\frac{π}{2}$,k∈Z,可得解得:k$π-\frac{7π}{12}$≤x≤kπ-$\frac{π}{12}$,k∈Z,
∴f(x)的递增区间为$[{kπ-\frac{7π}{12},kπ-\frac{π}{12}}]$,k∈Z.
(2)∵$f(C)=sin(2C+\frac{2π}{3})=-\frac{{\sqrt{3}}}{2}$,
∴$2C+\frac{2π}{3}=\frac{4π}{3}$或$\frac{5π}{3}$,解得$C=\frac{π}{3}$或$\frac{π}{2}$.
∵$\overrightarrow m=(1,sinA)$与$\overrightarrow n=(2,sinB)$共线,
∴sinB-2sinA=0,
∴由正弦定理可得$\frac{a}{b}=\frac{sinA}{sinB}=\frac{1}{2}$,即b=2a,①
当$C=\frac{π}{3}$时,
∵C=3,∴由余弦定理可得$9={a^2}+{b^2}-2abcos\frac{π}{3}$,②
联立①②解方程组可得$\left\{\begin{array}{l}a=\sqrt{3}\\ b=2\sqrt{3}\end{array}\right.$
当$C=\frac{π}{2}$时,
∵c=3,∴由勾股定理可得9=a2+b2,③
联立①③可得$a=\frac{{3\sqrt{5}}}{5}$,$b=\frac{{6\sqrt{5}}}{5}$,
综上$a=\sqrt{3}$,$b=2\sqrt{3}$,或$a=\frac{{3\sqrt{5}}}{5}$,$b=\frac{{6\sqrt{5}}}{5}$.
点评 本题主要考查了三角函数恒等变换的应用,正弦定理,余弦定理,勾股定理,平面向量共线的性质在解三角形中的应用,考查了计算能力和转化思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2或-1 | B. | 2 | C. | -1 | D. | 2或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{1}{2})$ | B. | [$\frac{1}{4},\frac{1}{2}$) | C. | ($\frac{1}{4},\frac{1}{2}$) | D. | ($0,\frac{1}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
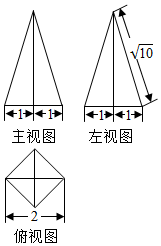 一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )
一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{3}$,$\frac{4}{3}$) | B. | (1,4) | C. | ($\frac{5}{3}$,$\frac{7}{3}$) | D. | (5,7) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com