
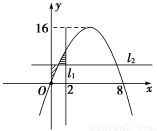
已知二次函数f(x)=ax2+bx+c,直线l1:x=2,直线l2:y=-t2+8t(其中0≤t≤2,t为常数),若直线l1,l2与函数f(x)的图象以及l1、l2、y轴与函数f(x)的图象所围成的封闭图形(阴影部分)如图所示.
(1)求a、b、c的值;
(2)求阴影面积S关于t的函数S(t)的解析式.
(1)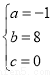 ;(2)
;(2)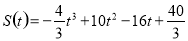
【解析】
试题分析:(1)根据二次函数过点 并且最大为16,列方程组解
并且最大为16,列方程组解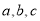 ;(2)定积分的基本思想的核心是“以直代曲”,用“有限”步骤解决“无限”问题,其方法是“分割求近似,求和取极限”,定积分只与积分区间和被积函数有关,与积分变量有关;(3)利用定积分求曲线围成图形的面积的步骤:一根据题意画简图;二确定被积函数;三确定积分的上限和下限,并求出交点坐标;四是运用微积分基本定理计算定积分,求出平面图形的面积;(4)求解时,注意要把定积分与利用定积分计算的曲线围成图形的面积区别开:定积分是一个数值,可为正,为负,也可以为零,而平面图形的面积在一般意义上总为正.
;(2)定积分的基本思想的核心是“以直代曲”,用“有限”步骤解决“无限”问题,其方法是“分割求近似,求和取极限”,定积分只与积分区间和被积函数有关,与积分变量有关;(3)利用定积分求曲线围成图形的面积的步骤:一根据题意画简图;二确定被积函数;三确定积分的上限和下限,并求出交点坐标;四是运用微积分基本定理计算定积分,求出平面图形的面积;(4)求解时,注意要把定积分与利用定积分计算的曲线围成图形的面积区别开:定积分是一个数值,可为正,为负,也可以为零,而平面图形的面积在一般意义上总为正.
试题解析:(1)由图形可知二次函数的图象过点(0,0),(8,0),并且f(x)的最大值为16,则
 ,解得
,解得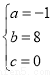 6分
6分
∴函数f(x)的解析式为f(x)=-x2+8x. 7分
(2)由 ,得x2-8x-t(t-8)=0,
,得x2-8x-t(t-8)=0,
∴x1=t,x2=8-t,
∵0≤t≤2,∴直线l2与f(x)的图象的交点坐标为(t,-t2+8t)由定积分的几何意义知:
S(t)=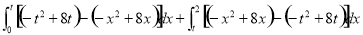
=[(-t2+8t)x-(-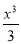 +4x2)]
+4x2)]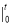 +[(-
+[(-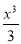 +4x2)-(-t2+8t)x]
+4x2)-(-t2+8t)x]
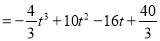 .
.
考点:(1)求二次函数的解析式;(2)利用定积分求阴影部分的面积


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源:2015届安徽省皖南八校高三第一次联考文科数学试卷(解析版) 题型:选择题
已知向量a,b满足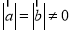 ,且关于x的函数,
,且关于x的函数,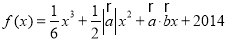 在R上有极值,则
在R上有极值,则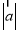 与
与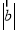 的夹角
的夹角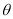 的取值范围为( )
的取值范围为( )
A.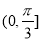 B.
B. 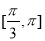 C.
C. 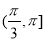 D.
D. 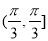
查看答案和解析>>
科目:高中数学 来源:2015届安徽省皖南八校高三第一次联考文科数学试卷(解析版) 题型:选择题
设全集U={-2,-1,1,2,3},集合A={-1,1,2},B={-1,1}则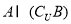 =( )
=( )
A.{1} B.{2} C.{1,2} D. {-1,1}
查看答案和解析>>
科目:高中数学 来源:2015届安徽省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
形如45132的数称为“波浪数”,即十位数字,千位数字均比与它们各自相邻的数字大,则由1,2,3,4,5可构成不重复的五位“波浪数”的个数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com