
设函数f(x)=ax2+bx+c(a,b,c∈R).若x=-1为函数f(x)ex的一个极值点,则下列图象不可能为y=f(x)的图象是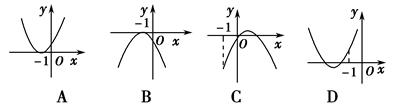
D
解析试题分析:由y=f(x)ex=ex(ax2+bx+c)⇒y'=f'(x)ex+exf(x)=ex[ax2+(b+2a)x+b+c],
由x=-1为函数f(x)ex的一个极值点可得,-1是方程ax2+(b+2a)x+b+c=0的一个根,
所以有a-(b+2a)+b+c=0⇒c=a.
法一:所以函数f(x)=ax2+bx+a,对称轴为x=- ,且f(-1)=2a-b,f(0)=a.
,且f(-1)=2a-b,f(0)=a.
对于A,由图得a>0,f(0)>0,f(-1)=0符合要求,
对于B,由图得a<0,f(0)<0,f(-1)=0不矛盾,
对于C,由图得a<0,f(0)<0,x=- >0得到b>0,f(-1)<0不矛盾,
>0得到b>0,f(-1)<0不矛盾,
对于D,由图得a>0,f(0)>0,x=- <-1得到b>2a,f(-1)<0于图中f(-1)>0矛盾,D不对.
<-1得到b>2a,f(-1)<0于图中f(-1)>0矛盾,D不对.
法二:得到函数f(x)=ax2+bx+a,由此得函数相应方程的两根之积为1,对照四个选项发现,D不成立,故选 D.
考点:本题主要考查应用导数研究函数的极值,二次函数图象和性质。
点评:易错题,本题要求“不可能”为的图象。研究函数的单调性、极值是导数的基本应用,方法明确,步骤规范。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com