分析:(1)利用线面垂直的判定定理和性质定理即可证明;
(2)证法一:利用线面平行的判定定理即可证明;证法二:利用面面平行的判定定理.
解答:证明:(1)∵AA
1⊥平面ABC,∴AA
1⊥BC,
又∵AC⊥BC,AA
1∩AC=A,
∴BC⊥平面AA
1C
1C,
∴BC⊥AC
1.
(2)解法一:当AF=3FC时,EF∥平面AA
1B
1B.
证明如下:在平A
1B
1C
1内过E作EG∥A
1C
1交A
1B
1于G,连接AG.
∵B
1E=3EC
1,∴
==,
又AF∥A
1C
1且
==
,
∴AF∥EG且AF=EG,
∴四边形AFEG为平行四边形,∴EF∥GA,
又∵EF?面AA
1B
1B,AG?平面AA
1B
1B,
∴EF∥平面AA
1B
1B.
解法二:当AF=3FC时,FE∥平面A
1ABB
1.
证明:在平面ABC内过E作EG∥BB
1交BC于G,连接FG.
∵EG∥BB
1,EG?A
1ABB
1,BB
1?平面A
1ABB
1,
∴EG∥平面A
1ABB
1.
∵B
1E=3EC
1,∴BG=3GC.
∴FG∥AB,
又AB?平面A
1ABB
1,FG?平面A
1ABB
1.
∴FG∥平面A
1ABB
1.
又EG∩FG=F,
∴平面EFG∥平面A
1ABB
1.
∴EF∥平面A
1ABB
1.
点评:熟练掌握线面、面面平行和垂直的判定定理和性质定理是解题的关键.

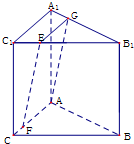
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC⊥BC,E、F分别在线段B1C1和AC上,B1E=3EC1,AC=BC=CC1=4
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AC⊥BC,E、F分别在线段B1C1和AC上,B1E=3EC1,AC=BC=CC1=4 (2)解法一:当AF=3FC时,EF∥平面AA1B1B.
(2)解法一:当AF=3FC时,EF∥平面AA1B1B.

 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( ) 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.